SphereAdaSTEM model: spherical indexing and modeling¶

Yangkang Chen
Jan 24, 2024

This notebook is to show the main difference of SphereAdaSTEM compared to AdaSTEM. To be specific, only the gridding part is different, and all other functionalities are inherited from AdaSTEM class. For complete functionality, please refer to AdaSTEM Demo.

We will explore the same modeling task as AdaSTEM Demo did: Predict the abundance of Mallard (a bird species) based on environmental variables. The data were requested from eBird, a citizen science project for bird observation, and with some variable annotation.

In [1]:

import pandas as pd
import numpy as np
import random
from tqdm.auto import tqdm
import matplotlib.pyplot as plt
import matplotlib
import warnings
import pickle
import os
import h3pandas

pd.set_option('display.max_columns', None)
# warnings.filterwarnings('ignore')

import pandas as pd import numpy as np import random from tqdm.auto import tqdm import matplotlib.pyplot as plt import matplotlib import warnings import pickle import os import h3pandas pd.set_option('display.max_columns', None) # warnings.filterwarnings('ignore')

In [2]:

%load_ext autoreload
%autoreload 2

%load_ext autoreload %autoreload 2

Download data¶

Training/test data¶

Please download the sample data from:

• Mallard: https://figshare.com/articles/dataset/Sample_data_Mallard_csv/24080745
  

Suppose now it's downloaded and saved as './Sample_data_Mallard.csv'

Alternatively, you can try other species like

• Alder Flycatcher: https://figshare.com/articles/dataset/Sample_data_Alder_Flycatcher_csv/24080751
  
• Short-eared Owl: https://figshare.com/articles/dataset/Sample_data_Short-eared_Owl_csv/24080742
  
• Eurasian Tree Sparrow: https://figshare.com/articles/dataset/Sample_data_Eurasian_Tree_Sparrow_csv/24080748
  

Caveat: These bird observation data are about 200MB each file.

In [3]:

data = pd.read_csv(f'./Sample_data_Mallard.csv')
data = data.drop('sampling_event_identifier', axis=1)

data = pd.read_csv(f'./Sample_data_Mallard.csv') data = data.drop('sampling_event_identifier', axis=1)

Prediction set¶

Prediction set are used to feed into a trained AdaSTEM model and make prediction: at some location, at some day of year, given the environmental variables, how many Mallard individual do I expected to observe?

The prediction set will be loaded after the model is trained.

Download the prediction set from: https://figshare.com/articles/dataset/Predset_2020_csv/24124980

Caveat: The file is about 700MB.

Get X and y¶

In [4]:

X = data.drop('count', axis=1)
y = data['count'].values

X = data.drop('count', axis=1) y = data['count'].values

In [5]:

X.head()

X.head()

Out[5]:

	longitude	latitude	DOY	duration_minutes	Traveling	Stationary	Area	effort_distance_km	number_observers	obsvr_species_count	time_observation_started_minute_of_day	elevation_mean	slope_mean	eastness_mean	northness_mean	bio1	bio2	bio3	bio4	bio5	bio6	bio7	bio8	bio9	bio10	bio11	bio12	bio13	bio14	bio15	bio16	bio17	bio18	bio19	closed_shrublands	cropland_or_natural_vegetation_mosaics	croplands	deciduous_broadleaf_forests	deciduous_needleleaf_forests	evergreen_broadleaf_forests	evergreen_needleleaf_forests	grasslands	mixed_forests	non_vegetated_lands	open_shrublands	permanent_wetlands	savannas	urban_and_built_up_lands	water_bodies	woody_savannas	entropy
0	-83.472224	8.859308	22	300.0	1	0	0	4.828	5.0	34.0	476	7.555556	0.758156	0.036083	-0.021484	24.883502	5.174890	59.628088	93.482247	30.529131	21.850519	8.678612	24.302626	26.536822	26.213334	23.864924	0.720487	0.127594	0.003156	0.001451	0.332425	0.026401	0.044218	0.260672	0.0	0.000000	0.0	0.0	0.0	0.138889	0.000000	0.000000	0.000000	0.0	0.0	0.777778	0.000000	0.000000	0.083333	0.000000	0.676720
1	-2.687724	43.373323	290	90.0	1	0	0	0.570	2.0	151.0	1075	30.833336	3.376527	0.050544	-0.099299	14.107917	5.224109	31.174167	376.543853	23.219421	6.461607	16.757814	9.048385	19.092725	19.236082	9.287841	0.171423	0.035598	0.004512	0.000081	0.084657	0.018400	0.030210	0.065007	0.0	0.000000	0.0	0.0	0.0	0.333333	0.000000	0.000000	0.083333	0.0	0.0	0.000000	0.194444	0.027778	0.000000	0.361111	1.359063
2	-89.884770	35.087255	141	10.0	0	1	0	-1.000	2.0	678.0	575	91.777780	0.558100	-0.187924	-0.269078	17.396487	8.673912	28.688889	718.996078	32.948335	2.713938	30.234397	14.741099	13.759220	26.795849	7.747272	0.187089	0.031802	0.005878	0.000044	0.073328	0.026618	0.039616	0.059673	0.0	0.055556	0.0	0.0	0.0	0.000000	0.000000	0.305556	0.000000	0.0	0.0	0.000000	0.527778	0.000000	0.000000	0.111111	1.104278
3	-99.216873	31.218510	104	9.0	1	0	0	0.805	2.0	976.0	657	553.166700	0.856235	-0.347514	-0.342971	20.740836	10.665164	35.409121	666.796919	35.909941	5.790119	30.119822	18.444353	30.734456	29.546417	11.701038	0.084375	0.025289	0.000791	0.000052	0.052866	0.004096	0.006064	0.015965	0.0	0.000000	0.0	0.0	0.0	0.000000	0.000000	1.000000	0.000000	0.0	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	-0.000000
4	-124.426730	43.065847	96	30.0	1	0	0	0.161	2.0	654.0	600	6.500000	0.491816	-0.347794	-0.007017	11.822340	6.766870	35.672897	396.157833	22.608788	3.639569	18.969219	8.184412	16.290802	17.258721	7.319234	0.144122	0.044062	0.000211	0.000147	0.089238	0.004435	0.004822	0.040621	0.0	0.000000	0.0	0.0	0.0	0.361111	0.166667	0.000000	0.472222	0.0	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	1.020754

The features include:

• spatial coordinates:

  • longitude and latitude (used for indexing, not actual training)

• Temporal coordinate:

  • day of year (DOY): used for both indexing and training

• Sampling parameters: These are parameters quantifying how the observation was made

  • duration_minutes: How long the observation was conducted
  • Observation protocol: Traveling, Stationary, or Area
  • effort_distance_km: how far have one traveled
  • number_observers: How many observers are there in the group
  • obsvr_species_count: How many bird species have the birder observed in the past
  • time_observation_started_minute_of_day: When did the birder start birding

• Topological features:

  • Features of elevation: elevation_mean
  • Features of slope magnitude and direction: slope_mean, eastness_mean, northness_mean

• Bioclimate features:

  • Summaries of yearly temperature and precipitation: from bio1 to bio19

• Land cover features:

  • Summaries of land cover, percentage of cover. For example, closed_shrublands, urban_and_built_up_lands.
  • entropy: Entropy of land cover

As you can see, the environmental variables are almost static. However, dynamic features (e.g., daily temperature) is fully supported as input. See Tips for data types for details.

Now we can take a look at the target variable

In [6]:

plt.hist(np.log(y+1),bins=100)
plt.xlabel('log count')
plt.show()

zero_frac = np.sum(y==0)/len(y)
print(f'Percentage record with zero Mallard count: {zero_frac*100}%')

plt.hist(np.log(y+1),bins=100) plt.xlabel('log count') plt.show() zero_frac = np.sum(y==0)/len(y) print(f'Percentage record with zero Mallard count: {zero_frac*100}%')

Percentage record with zero Mallard count: 83.09425%

The target data is extremely zero-inflated. 83% checklists have not Mallard observation. This poses the necessity of using hurdle model.

First thing first: Spatiotemporal train test split¶

In [7]:

from stemflow.model_selection import ST_train_test_split
X_train, X_test, y_train, y_test = ST_train_test_split(X, y, 
                                                        Spatio1 = 'longitude',
                                                        Spatio2 = 'latitude',
                                                        Temporal1 = 'DOY',
                                                        Spatio_blocks_count = 50, Temporal_blocks_count=50,
                                                        random_state=42, test_size=0.3)

from stemflow.model_selection import ST_train_test_split X_train, X_test, y_train, y_test = ST_train_test_split(X, y, Spatio1 = 'longitude', Spatio2 = 'latitude', Temporal1 = 'DOY', Spatio_blocks_count = 50, Temporal_blocks_count=50, random_state=42, test_size=0.3)

This makes sure that we have a held-out test set, so that the estimation will be reliable.

For details of parameter setting, see AdaSTEM Demo.

Train AdaSTEM hurdle model¶

In [8]:

from stemflow.model.SphereAdaSTEM import SphereAdaSTEM, SphereAdaSTEMClassifier, SphereAdaSTEMRegressor
from xgboost import XGBClassifier, XGBRegressor # remember to install xgboost if you use it as base model
from stemflow.model.Hurdle import Hurdle_for_AdaSTEM, Hurdle

from stemflow.model.SphereAdaSTEM import SphereAdaSTEM, SphereAdaSTEMClassifier, SphereAdaSTEMRegressor from xgboost import XGBClassifier, XGBRegressor # remember to install xgboost if you use it as base model from stemflow.model.Hurdle import Hurdle_for_AdaSTEM, Hurdle

We first import the models. Although some classes are not used, I imported them for complete showcase of function.

Here, we import the SphereAdaSTEM, SphereAdaSTEMClassifier and SphereAdaSTEMRegressor from stemflow.model.SphereAdaSTEM module.

In [9]:

## "hurdle in Ada"
model = SphereAdaSTEMRegressor(
    base_model=Hurdle(
        classifier=XGBClassifier(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1),
        regressor=XGBRegressor(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1)
    ),                                      # hurdel model for zero-inflated problem (e.g., count)
    save_gridding_plot = True,
    ensemble_fold=10,                       # data are modeled 10 times, each time with jitter and rotation in Quadtree algo
    min_ensemble_required=7,                # Only points covered by > 7 stixels will be predicted
    grid_len_upper_threshold=2500,            # force splitting if the grid length exceeds 2500 (km)
    grid_len_lower_threshold=500,             # stop splitting if the grid length fall short 500 (km)        
    temporal_start=1,                       # The next 4 params define the temporal sliding window
    temporal_end=366,                            
    temporal_step=25,                       # The window takes steps of 20 DOY (see AdaSTEM demo for details)
    temporal_bin_interval=50,               # Each window will contain data of 50 DOY
    points_lower_threshold=50,              # Only stixels with more than 50 samples are trained
    Temporal1='DOY',
    use_temporal_to_train=True,             # In each stixel, whether 'DOY' should be a predictor
    n_jobs=1
)

## "hurdle in Ada" model = SphereAdaSTEMRegressor( base_model=Hurdle( classifier=XGBClassifier(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1), regressor=XGBRegressor(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1) ), # hurdel model for zero-inflated problem (e.g., count) save_gridding_plot = True, ensemble_fold=10, # data are modeled 10 times, each time with jitter and rotation in Quadtree algo min_ensemble_required=7, # Only points covered by > 7 stixels will be predicted grid_len_upper_threshold=2500, # force splitting if the grid length exceeds 2500 (km) grid_len_lower_threshold=500, # stop splitting if the grid length fall short 500 (km) temporal_start=1, # The next 4 params define the temporal sliding window temporal_end=366, temporal_step=25, # The window takes steps of 20 DOY (see AdaSTEM demo for details) temporal_bin_interval=50, # Each window will contain data of 50 DOY points_lower_threshold=50, # Only stixels with more than 50 samples are trained Temporal1='DOY', use_temporal_to_train=True, # In each stixel, whether 'DOY' should be a predictor n_jobs=1 )

The parameter setting is mostly similar to AdaSTEM. The differences is that:

1. We use SphereAdaSTEMRegressor as regressor, and
2. We set grid_len_upper_threshold and grid_len_lower_threshold as real distance in kilometers, although the spatial columns are longitude and latitude.
3. You must have a column named "longitude" and a column named "latitude" in you dataframe. The grid will be generated on the fly, and gridding will be based on real distance.

For other details of parameter setting, see AdaSTEM Demo.

We then fit the model by simply call:

In [10]:

# columns of X_train should only contain predictors and Spatio-temporal indicators ('longitude', 'latitude', Temporal1)
model.fit(X_train.reset_index(drop=True), y_train, verbosity=1)

# columns of X_train should only contain predictors and Spatio-temporal indicators ('longitude', 'latitude', Temporal1) model.fit(X_train.reset_index(drop=True), y_train, verbosity=1)

Generating Ensemble: 100%|██████████| 10/10 [07:21<00:00, 44.14s/it]

training:   0%|          | 0/10 [00:00<?, ?it/s]

Out[10]:

SphereAdaSTEMRegressor(base_model=Hurdle(classifier=XGBClassifier(base_score=None,
                                                                  booster=None,
                                                                  callbacks=None,
                                                                  colsample_bylevel=None,
                                                                  colsample_bynode=None,
                                                                  colsample_bytree=None,
                                                                  early_stopping_rounds=None,
                                                                  enable_categorical=False,
                                                                  eval_metric=None,
                                                                  feature_types=None,
                                                                  gamma=None,
                                                                  gpu_id=None,
                                                                  grow_policy=None,
                                                                  importance_type=None,
                                                                  interaction_constraints=...
                                                                max_bin=None,
                                                                max_cat_threshold=None,
                                                                max_cat_to_onehot=None,
                                                                max_delta_step=None,
                                                                max_depth=None,
                                                                max_leaves=None,
                                                                min_child_weight=None,
                                                                missing=nan,
                                                                monotone_constraints=None,
                                                                n_estimators=100,
                                                                n_jobs=1,
                                                                num_parallel_tree=None,
                                                                predictor=None,
                                                                random_state=42, ...)),
                       grid_len_upper_threshold=2500, save_gridding_plot=True,
                       stixel_training_size_threshold=50, temporal_step=25)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Plot QuadTree ensembles¶

In [11]:

model.gridding_plot

model.gridding_plot

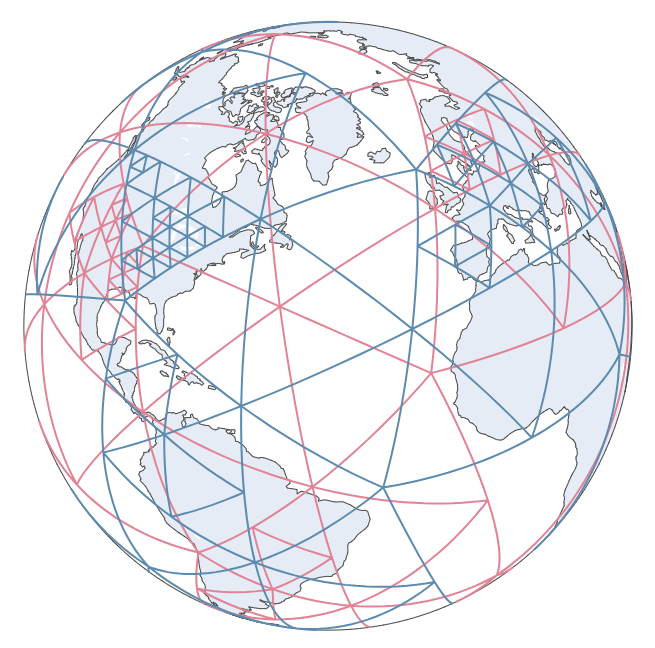
Here for an interactive plot Interactive spherical gridding plot.

In [12]:

with open('sphere_gridding_plot.html','w') as f:
    f.write(model.gridding_plot.to_html())

with open('sphere_gridding_plot.html','w') as f: f.write(model.gridding_plot.to_html())

This shows the 10 Quadtree ensembles we made. Region with higher data volume were split into smaller gird. The grid length is constrained between (500, 2500) kilometers.

Feature importances¶

After training the model, now we are interested in what features are important in bird abundance prediction

In [13]:

# Calcualte feature importance.
model.calculate_feature_importances()
# stixel-specific feature importance is saved in model.feature_importances_

# Calcualte feature importance. model.calculate_feature_importances() # stixel-specific feature importance is saved in model.feature_importances_

In [14]:

top10_features = model.feature_importances_.iloc[:,1:].rank(axis=1).mean(axis=0).sort_values(ascending=False).head(10)
top10_features

top10_features = model.feature_importances_.iloc[:,1:].rank(axis=1).mean(axis=0).sort_values(ascending=False).head(10) top10_features

Out[14]:

slope_mean             34.278389
effort_distance_km     33.836596
elevation_mean         32.857154
northness_mean         30.856551
bio4                   30.786596
eastness_mean          30.688630
duration_minutes       30.666340
obsvr_species_count    30.222590
bio8                   29.530572
bio2                   29.444051
dtype: float64

slope_mean, effort_distance_km, and elevation_mean are the top 3 predictors of Mallard abundance across the sampled space and time.

The feature importance ranking is similar to the results of AdaSTEM.

Evaluation¶

Now, we evaluate our overall model performance on the held-out test set:

In [15]:

pred = model.predict(X_test, verbosity=1)

pred = model.predict(X_test, verbosity=1)

predicting:   0%|          | 0/10 [00:00<?, ?it/s]

The samples not predictable are output as np.nan:

In [16]:

perc = np.sum(np.isnan(pred.flatten()))/len(pred.flatten())
print(f'Percentage not predictable {round(perc*100, 2)}%')

perc = np.sum(np.isnan(pred.flatten()))/len(pred.flatten()) print(f'Percentage not predictable {round(perc*100, 2)}%')

Percentage not predictable 0.02%

More points are predictable compared to AdaSTEM model (0.02% unpredictable compared to ~1% unpredictable)! This is expected, as the Sphere indexing system enclose almost every corner of the earth.

We evaluate the performance using various metrics implemented in SphereAdaSTEM.eval_STEM_res or AdaSTEM.eval_STEM_res method:

In [17]:

pred_df = pd.DataFrame({
    'y_true':y_test.flatten(),
    'y_pred':np.where(pred.flatten()<0, 0, pred.flatten())
}).dropna()

SphereAdaSTEM.eval_STEM_res('hurdle', pred_df.y_true, pred_df.y_pred)

pred_df = pd.DataFrame({ 'y_true':y_test.flatten(), 'y_pred':np.where(pred.flatten()<0, 0, pred.flatten()) }).dropna() SphereAdaSTEM.eval_STEM_res('hurdle', pred_df.y_true, pred_df.y_pred)

Out[17]:

{'AUC': 0.7709769441127502,
 'kappa': 0.40418935376349774,
 'f1': 0.5315554903435247,
 'precision': 0.4095122364777031,
 'recall': 0.7572242253226733,
 'average_precision': 0.35007503024002873,
 'Spearman_r': 0.47773497480632715,
 'Pearson_r': 0.20838678841242564,
 'R2': -0.010718003793811492,
 'MAE': 4.0526054794665,
 'MSE': 1270.2122920088268,
 'poisson_deviance_explained': 0.14793642063493806}

The model performance is similar compared to AdaSTEM model. The model performance should mainly be a result of parameters like ensemble_fold and points_lower_threshold, rather than the 2D or 3D gridding system.

Save model¶

We use pickle to save the model:

In [18]:

with open('./01.demo_adastem_model.pkl','wb') as f:
    pickle.dump(model, f)

with open('./01.demo_adastem_model.pkl','wb') as f: pickle.dump(model, f)

To load the model, do:

In [19]:

with open('./01.demo_adastem_model.pkl','rb') as f:
    model = pickle.load(f)

with open('./01.demo_adastem_model.pkl','rb') as f: model = pickle.load(f)

Calculate memory usage¶

Finally, we are interested in how many disk space & memory our model consumed. stemflow is typically memory costly, especially when data volume and ensembles go up – the memory usage may also go up linearly. We do not currently provide solution for memory optimization. We well come PR to work on that.

In [20]:

# Calculate memory usage
model_size_G = round(os.path.getsize('./01.demo_adastem_model.pkl')/1024/1024/1024, 2)
training_data_memory_G = round(X.memory_usage().sum()/1024/1024/1024, 2)

# Calculate model info
true_hurdle_model_count = np.sum([1 if isinstance(model.model_dict[i].classifier, XGBClassifier) else 0 for i in model.model_dict])
dummy_model_count = len(model.model_dict) - true_hurdle_model_count
true_hurdle_model_perc = round(true_hurdle_model_count/len(model.model_dict) * 100, 2)
dummy_model_perc = round(dummy_model_count/len(model.model_dict) * 100, 2)

# Calculate memory usage model_size_G = round(os.path.getsize('./01.demo_adastem_model.pkl')/1024/1024/1024, 2) training_data_memory_G = round(X.memory_usage().sum()/1024/1024/1024, 2) # Calculate model info true_hurdle_model_count = np.sum([1 if isinstance(model.model_dict[i].classifier, XGBClassifier) else 0 for i in model.model_dict]) dummy_model_count = len(model.model_dict) - true_hurdle_model_count true_hurdle_model_perc = round(true_hurdle_model_count/len(model.model_dict) * 100, 2) dummy_model_perc = round(dummy_model_count/len(model.model_dict) * 100, 2)

In [21]:

print(f"""
      
      This AdaSTEM model have {len(model.model_dict)} trained based models in total.
      Among them, {dummy_model_count} ({dummy_model_perc}%) are dummy models that always predict one class (because the input data labels are homogeneous).
      Oppositely, {true_hurdle_model_count} ({true_hurdle_model_perc}%) are true hurdle models.
      
      The input data consume {training_data_memory_G} G memory.
      The model takes {model_size_G} G space on the disks.
      
""")

print(f""" This AdaSTEM model have {len(model.model_dict)} trained based models in total. Among them, {dummy_model_count} ({dummy_model_perc}%) are dummy models that always predict one class (because the input data labels are homogeneous). Oppositely, {true_hurdle_model_count} ({true_hurdle_model_perc}%) are true hurdle models. The input data consume {training_data_memory_G} G memory. The model takes {model_size_G} G space on the disks. """)

      
      This AdaSTEM model have 6640 trained based models in total.
      Among them, 1229 (18.51%) are dummy models that always predict one class (because the input data labels are homogeneous).
      Oppositely, 5411 (81.49%) are true hurdle models.
      
      The input data consume 0.15 G memory.
      The model takes 1.7 G space on the disks.
      

Conclusion¶

Although we cannot directly compare the speed and performance of two modeling framework with different parameter settings, the results definitely show that, with similar gridding parameters:

For training:

1. AdaSTEM and SphereAdaSTEM have similar speed.
2. SphereAdaSTEM spends longer on gridding, but not significantly.

For prediction:

1. SphereAdaSTEM has higher coverage, and therefore more samples in the test set can be predicted.
2. The prediction speed of SphereAdaSTEM is almost double slower than AdaSTEM.
3. The model performance is similar in terms of all metrics.

For memory use:

1. The two model consume similar amount of memory.

My suggestion is that:

1. For local modeling, you could use AdaSTEM for simplicity and understandability.
2. For global modeling, if you don't mind the difference in speed, you can use SphereAdaSTEM.
3. For samples that distributed much towards the poles, definitely use SphereAdaSTEM.

Please open an issue if you have any question

Cheers!

In [22]:

from watermark import watermark
print(watermark())
print(watermark(packages="stemflow,numpy,scipy,pandas,xgboost,tqdm,matplotlib,h3pandas,geopandas,scikit-learn"))

from watermark import watermark print(watermark()) print(watermark(packages="stemflow,numpy,scipy,pandas,xgboost,tqdm,matplotlib,h3pandas,geopandas,scikit-learn"))

Last updated: 2024-01-24T21:47:37.851624+08:00

Python implementation: CPython
Python version       : 3.9.7
IPython version      : 8.14.0

Compiler    : Clang 11.1.0 
OS          : Darwin
Release     : 21.6.0
Machine     : arm64
Processor   : arm
CPU cores   : 8
Architecture: 64bit

stemflow    : 1.0.9.4
numpy       : 1.24.3
scipy       : 1.10.1
pandas      : 2.0.3
xgboost     : 1.7.6
tqdm        : 4.65.0
matplotlib  : 3.7.1
h3pandas    : 0.2.4
geopandas   : 0.11.1
scikit-learn: 0.0