A demo of AdaSTEM model¶

Yangkang Chen
Oct 26, 2024

This notebook is to provide a simple demonstration of how to use stemflow for AdaSTEM modeling.

For spherical indexing, see SphereAdaSTEM demo.

We will explore a modeling task: Predict the abundance of Mallard (a bird species) based on environmental variables. The data were requested from eBird, a citizen science project for bird observation, and with some variable annotation.

In [1]:

import os
import sys 

import pandas as pd
import numpy as np
import random
from tqdm.auto import tqdm
import matplotlib.pyplot as plt
import matplotlib
import warnings
import pickle
import h3pandas

pd.set_option('display.max_columns', None)
# warnings.filterwarnings('ignore')

import os import sys import pandas as pd import numpy as np import random from tqdm.auto import tqdm import matplotlib.pyplot as plt import matplotlib import warnings import pickle import h3pandas pd.set_option('display.max_columns', None) # warnings.filterwarnings('ignore')

In [2]:

%load_ext autoreload
%autoreload 2

%load_ext autoreload %autoreload 2

Download data¶

Training/test data¶

Please download the sample data from:

• Mallard: https://figshare.com/articles/dataset/Sample_data_Mallard_csv/24080745
  

Suppose now it's downloaded and saved as './Sample_data_Mallard.csv'

Alternatively, you can try other species like

• Alder Flycatcher: https://figshare.com/articles/dataset/Sample_data_Alder_Flycatcher_csv/24080751
  
• Short-eared Owl: https://figshare.com/articles/dataset/Sample_data_Short-eared_Owl_csv/24080742
  
• Eurasian Tree Sparrow: https://figshare.com/articles/dataset/Sample_data_Eurasian_Tree_Sparrow_csv/24080748
  

Caveat: These bird observation data are about 200MB each file.

In [3]:

data = pd.read_csv(f'./Sample_data_Mallard.csv')
data = data.drop('sampling_event_identifier', axis=1)

data = pd.read_csv(f'./Sample_data_Mallard.csv') data = data.drop('sampling_event_identifier', axis=1)

Prediction set¶

Prediction set are used to feed into a trained AdaSTEM model and make prediction: at some location, at some day of year, given the environmental variables, how many Mallard individual do I expected to observe?

The prediction set will be loaded after the model is trained.

Download the prediction set from: https://figshare.com/articles/dataset/Predset_2020_csv/24124980

Caveat: The file is about 700MB.

Get X and y¶

In [4]:

X = data.drop('count', axis=1)
y = data['count'].values

X = data.drop('count', axis=1) y = data['count'].values

In [5]:

X.head()

X.head()

Out[5]:

	longitude	latitude	DOY	duration_minutes	Traveling	Stationary	Area	effort_distance_km	number_observers	obsvr_species_count	time_observation_started_minute_of_day	elevation_mean	slope_mean	eastness_mean	northness_mean	bio1	bio2	bio3	bio4	bio5	bio6	bio7	bio8	bio9	bio10	bio11	bio12	bio13	bio14	bio15	bio16	bio17	bio18	bio19	closed_shrublands	cropland_or_natural_vegetation_mosaics	croplands	deciduous_broadleaf_forests	deciduous_needleleaf_forests	evergreen_broadleaf_forests	evergreen_needleleaf_forests	grasslands	mixed_forests	non_vegetated_lands	open_shrublands	permanent_wetlands	savannas	urban_and_built_up_lands	water_bodies	woody_savannas	entropy
0	-83.472224	8.859308	22	300.0	1	0	0	4.828	5.0	34.0	476	7.555556	0.758156	0.036083	-0.021484	24.883502	5.174890	59.628088	93.482247	30.529131	21.850519	8.678612	24.302626	26.536822	26.213334	23.864924	0.720487	0.127594	0.003156	0.001451	0.332425	0.026401	0.044218	0.260672	0.0	0.000000	0.0	0.0	0.0	0.138889	0.000000	0.000000	0.000000	0.0	0.0	0.777778	0.000000	0.000000	0.083333	0.000000	0.676720
1	-2.687724	43.373323	290	90.0	1	0	0	0.570	2.0	151.0	1075	30.833336	3.376527	0.050544	-0.099299	14.107917	5.224109	31.174167	376.543853	23.219421	6.461607	16.757814	9.048385	19.092725	19.236082	9.287841	0.171423	0.035598	0.004512	0.000081	0.084657	0.018400	0.030210	0.065007	0.0	0.000000	0.0	0.0	0.0	0.333333	0.000000	0.000000	0.083333	0.0	0.0	0.000000	0.194444	0.027778	0.000000	0.361111	1.359063
2	-89.884770	35.087255	141	10.0	0	1	0	-1.000	2.0	678.0	575	91.777780	0.558100	-0.187924	-0.269078	17.396487	8.673912	28.688889	718.996078	32.948335	2.713938	30.234397	14.741099	13.759220	26.795849	7.747272	0.187089	0.031802	0.005878	0.000044	0.073328	0.026618	0.039616	0.059673	0.0	0.055556	0.0	0.0	0.0	0.000000	0.000000	0.305556	0.000000	0.0	0.0	0.000000	0.527778	0.000000	0.000000	0.111111	1.104278
3	-99.216873	31.218510	104	9.0	1	0	0	0.805	2.0	976.0	657	553.166700	0.856235	-0.347514	-0.342971	20.740836	10.665164	35.409121	666.796919	35.909941	5.790119	30.119822	18.444353	30.734456	29.546417	11.701038	0.084375	0.025289	0.000791	0.000052	0.052866	0.004096	0.006064	0.015965	0.0	0.000000	0.0	0.0	0.0	0.000000	0.000000	1.000000	0.000000	0.0	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	-0.000000
4	-124.426730	43.065847	96	30.0	1	0	0	0.161	2.0	654.0	600	6.500000	0.491816	-0.347794	-0.007017	11.822340	6.766870	35.672897	396.157833	22.608788	3.639569	18.969219	8.184412	16.290802	17.258721	7.319234	0.144122	0.044062	0.000211	0.000147	0.089238	0.004435	0.004822	0.040621	0.0	0.000000	0.0	0.0	0.0	0.361111	0.166667	0.000000	0.472222	0.0	0.0	0.000000	0.000000	0.000000	0.000000	0.000000	1.020754

The features include:

• spatial coordinates:

  • longitude and latitude (used for indexing, not actual training)

• Temporal coordinate:

  • day of year (DOY): used for both indexing and training

• Sampling parameters: These are parameters quantifying how the observation was made

  • duration_minutes: How long the observation was conducted
  • Observation protocol: Traveling, Stationary, or Area
  • effort_distance_km: how far have one traveled
  • number_observers: How many observers are there in the group
  • obsvr_species_count: How many bird species have the birder observed in the past
  • time_observation_started_minute_of_day: When did the birder start birding

• Topological features:

  • Features of elevation: elevation_mean
  • Features of slope magnitude and direction: slope_mean, eastness_mean, northness_mean

• Bioclimate features:

  • Summaries of yearly temperature and precipitation: from bio1 to bio19

• Land cover features:

  • Summaries of land cover, percentage of cover. For example, closed_shrublands, urban_and_built_up_lands.
  • entropy: Entropy of land cover

As you can see, the environmental variables are almost static. However, dynamic features (e.g., daily temperature) is fully supported as input. See Tips for data types for details.

Now we can take a look at the target variable

In [6]:

plt.hist(np.log(y+1),bins=100)
plt.xlabel('log count')
plt.show()

zero_frac = np.sum(y==0)/len(y)
print(f'Percentage record with zero Mallard count: {zero_frac*100}%')

plt.hist(np.log(y+1),bins=100) plt.xlabel('log count') plt.show() zero_frac = np.sum(y==0)/len(y) print(f'Percentage record with zero Mallard count: {zero_frac*100}%')

Percentage record with zero Mallard count: 83.09425%

The target data is extremely zero-inflated. 83% checklists have not Mallard observation. This poses the necessity of using hurdle model.

First thing first: Spatiotemporal train test split¶

In [7]:

from stemflow.model_selection import ST_train_test_split
X_train, X_test, y_train, y_test = ST_train_test_split(X, y, 
                                                        Spatio1 = 'longitude',
                                                        Spatio2 = 'latitude',
                                                        Temporal1 = 'DOY',
                                                        Spatio_blocks_count = 50, Temporal_blocks_count=50,
                                                        random_state=42, test_size=0.3)

from stemflow.model_selection import ST_train_test_split X_train, X_test, y_train, y_test = ST_train_test_split(X, y, Spatio1 = 'longitude', Spatio2 = 'latitude', Temporal1 = 'DOY', Spatio_blocks_count = 50, Temporal_blocks_count=50, random_state=42, test_size=0.3)

Here we used a spatiotemporal train-test-spit to split the data into different blocks.

As shown, longitude and latitude are split into 50 bins separately, and DOY is split into 50 bins as well.

We then randomly select 30% of the spatiotemporal blocks as test data, and the rest as training data.

That is, if the data X have longitude ranging from (-180, 180), latitude ranging from (-90, 90), and whole year data (1, 366), each block will approximately contain data of 7.2 longitude (about 800km), 3.6 latitude (about 400km), and 7 days, which approximately catch the spatiotemporal scale of bird migration. These are rough estimates to get a sense of the scale. Note: the actual geometry (in meter) of 1-degree longitude will change by the latitudinal positions. In that case, you may consider projecting your data to and equal-area coordinates. In our case, we believe that the bias induced by coordinate system is relatively low, considering the size of our grids (and this is the coordinate system used in the original AdaSTEM paper, although it is a apparent issue).

The underlying interpretation is that: the generalization performance to adjacent (800km, 400km, 7days) block is [TEST RESULT]. As the bin count getting larger, the bin size get smaller, and your estimation becoming more radical and optimistic.

You can input any coordinate and set different bins as long as they match your model assumption.

Train AdaSTEM hurdle model¶

In [8]:

from stemflow.model.AdaSTEM import AdaSTEM, AdaSTEMClassifier, AdaSTEMRegressor
from xgboost import XGBClassifier, XGBRegressor # remember to install xgboost if you use it as base model
from stemflow.model.Hurdle import Hurdle_for_AdaSTEM, Hurdle

from stemflow.model.AdaSTEM import AdaSTEM, AdaSTEMClassifier, AdaSTEMRegressor from xgboost import XGBClassifier, XGBRegressor # remember to install xgboost if you use it as base model from stemflow.model.Hurdle import Hurdle_for_AdaSTEM, Hurdle

We first import the models. Although some classes are not used, I imported them for complete showcase of function.

In [9]:

## "hurdle in Ada"
model = AdaSTEMRegressor(
    base_model=Hurdle(
        classifier=XGBClassifier(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1),
        regressor=XGBRegressor(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1)
    ),                                      # hurdel model for zero-inflated problem (e.g., count)
    save_gridding_plot = True,
    ensemble_fold=10,                       # data are modeled 10 times, each time with jitter and rotation in Quadtree algo
    min_ensemble_required=7,                # Only points covered by > 7 ensembles will be predicted
    grid_len_upper_threshold=25,            # force splitting if the grid length exceeds 25
    grid_len_lower_threshold=5,             # stop splitting if the grid length fall short 5         
    temporal_start=1,                       # The next 4 params define the temporal sliding window
    temporal_end=366,                            
    temporal_step=25,                       # The window takes steps of 20 DOY (see AdaSTEM demo for details)
    temporal_bin_interval=50,               # Each window will contain data of 50 DOY
    points_lower_threshold=50,              # Only stixels with more than 50 samples are trained
    Spatio1='longitude',                    # The next three params define the name of 
    Spatio2='latitude',                     # spatial coordinates shown in the dataframe
    Temporal1='DOY',
    use_temporal_to_train=True,             # In each stixel, whether 'DOY' should be a predictor
    n_jobs=1,                               # Not using parallel computing
    random_state=42,                        # The random state makes the gridding process reproducible
    lazy_loading=True                       # Using lazy loading for large ensemble amount (e.g., >20 ensembles). 
                                            # -- Each trained ensemble will be saved into disk and will only be loaded if needed (e.g. for prediction).
)

## "hurdle in Ada" model = AdaSTEMRegressor( base_model=Hurdle( classifier=XGBClassifier(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1), regressor=XGBRegressor(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1) ), # hurdel model for zero-inflated problem (e.g., count) save_gridding_plot = True, ensemble_fold=10, # data are modeled 10 times, each time with jitter and rotation in Quadtree algo min_ensemble_required=7, # Only points covered by > 7 ensembles will be predicted grid_len_upper_threshold=25, # force splitting if the grid length exceeds 25 grid_len_lower_threshold=5, # stop splitting if the grid length fall short 5 temporal_start=1, # The next 4 params define the temporal sliding window temporal_end=366, temporal_step=25, # The window takes steps of 20 DOY (see AdaSTEM demo for details) temporal_bin_interval=50, # Each window will contain data of 50 DOY points_lower_threshold=50, # Only stixels with more than 50 samples are trained Spatio1='longitude', # The next three params define the name of Spatio2='latitude', # spatial coordinates shown in the dataframe Temporal1='DOY', use_temporal_to_train=True, # In each stixel, whether 'DOY' should be a predictor n_jobs=1, # Not using parallel computing random_state=42, # The random state makes the gridding process reproducible lazy_loading=True # Using lazy loading for large ensemble amount (e.g., >20 ensembles). # -- Each trained ensemble will be saved into disk and will only be loaded if needed (e.g. for prediction). )

Here we used the Hurdle model as based model of AdaSTEMRegressor. For more discussion on modeling framework, see Tips for different tasks and Model structure of AdaSTEM and Hurdle.

During the "split-apply-combine" process, the data is first chunked into temporal windows by sliding window approach:

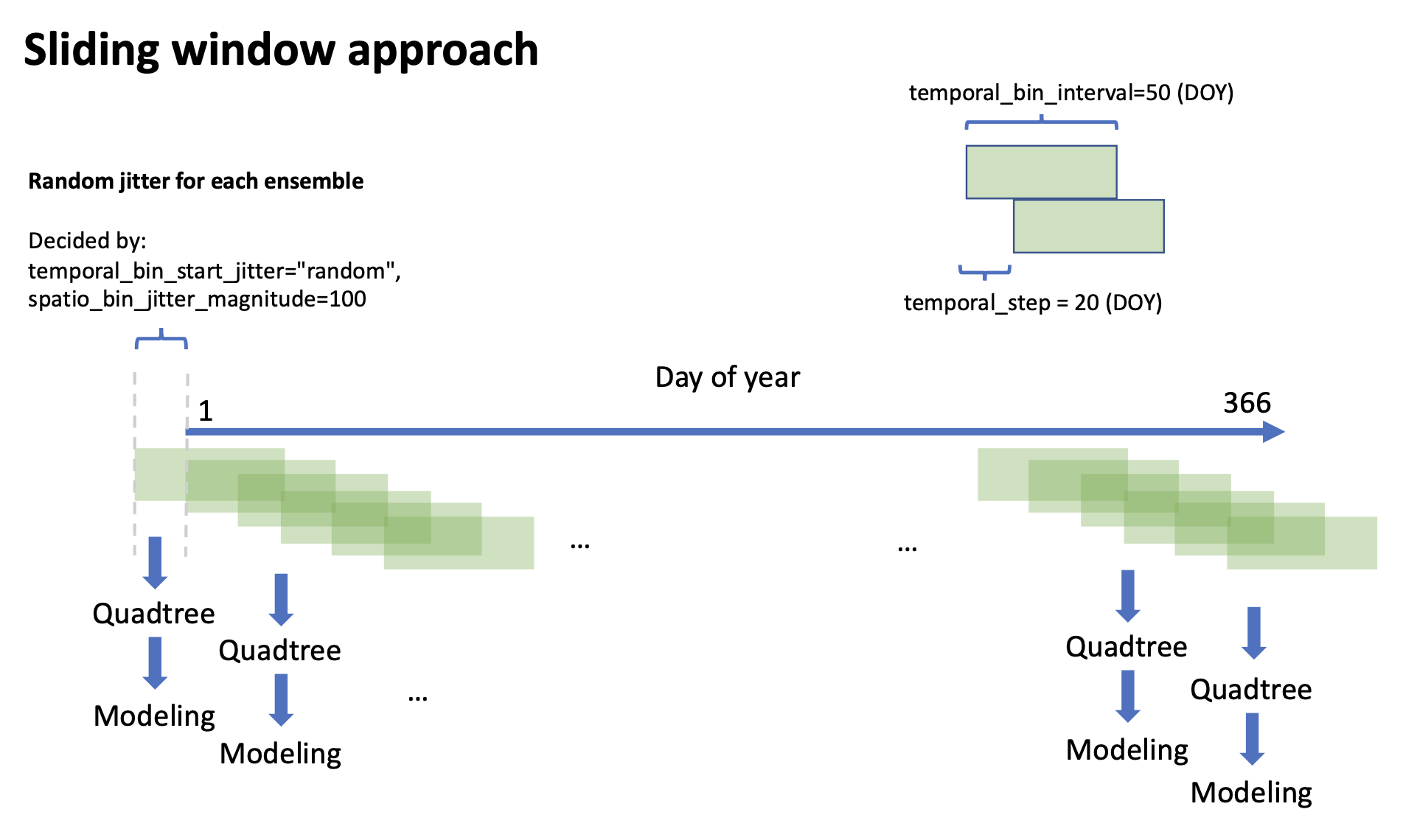
Then, for each temporal window, we split the data into spatial grids:

We choose adaptive grid size between 5 unit and 25 unit because these parameters was used in the original AdaSTEM paper. Large gird size will reduce the model performance (underfitting & over-extrapolation), and small gird size is likely overfitting to local condition. Likewise, we choose temporal window with size of 50 DOY and step of 25 DOY for that this timescale captures the onset and dynamics of migration. For more discussion on parameters please see Optimizing stixel size. We ask that only stixels with more than 50 samples are trained, to avoid incomplete sampling during bird survey. This is also recommended in the AdaSTEM paper. For rare/hard-to-observe species, the value should be set larger.

You could also use 3D spherical indexing, which is unbiased towards poles: SphereAdaSTEM demo.

We then fit the model by simply call:

In [10]:

# columns of X_train should only contain predictors and Spatio-temporal indicators (Spatio1, Spatio2, Temporal1)
model.fit(X_train.reset_index(drop=True), y_train, verbosity=1)

# columns of X_train should only contain predictors and Spatio-temporal indicators (Spatio1, Spatio2, Temporal1) model.fit(X_train.reset_index(drop=True), y_train, verbosity=1)

Generating Ensembles: 100%|██████████| 10/10 [00:16<00:00,  1.60s/it]
Training: 100%|██████████| 10/10 [09:28<00:00, 56.88s/it]

Out[10]:

AdaSTEMRegressor(base_model=Hurdle(classifier=XGBClassifier(base_score=None,
                                                            booster=None,
                                                            callbacks=None,
                                                            colsample_bylevel=None,
                                                            colsample_bynode=None,
                                                            colsample_bytree=None,
                                                            device=None,
                                                            early_stopping_rounds=None,
                                                            enable_categorical=False,
                                                            eval_metric=None,
                                                            feature_types=None,
                                                            gamma=None,
                                                            grow_policy=None,
                                                            importance_type=None,
                                                            interaction_constraints=None,
                                                            l...
                                                          monotone_constraints=None,
                                                          multi_strategy=None,
                                                          n_estimators=None,
                                                          n_jobs=1,
                                                          num_parallel_tree=None,
                                                          random_state=42, ...)),
                 lazy_loading=True,
                 lazy_loading_dir='stemflow_model_Q9sX3Sab53O6Cr78',
                 plot_xlims=(-179.8730564, 178.7306634),
                 plot_ylims=(-66.6730616, 73.0109413), random_state=42,
                 save_gridding_plot=True, stixel_training_size_threshold=50,
                 temporal_step=25)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

In [11]:

model.ensemble_df

model.ensemble_df

Out[11]:

	stixel_indexes	stixel_width	stixel_height	stixel_checklist_count	stixel_calibration_point(transformed)	rotation	ensemble_index	DOY_start	DOY_end	unique_stixel_id	stixel_calibration_point_transformed_left_bound	stixel_calibration_point_transformed_lower_bound	stixel_calibration_point_transformed_right_bound	stixel_calibration_point_transformed_upper_bound	calibration_point_x_jitter	calibration_point_y_jitter
0	5	22.239557	22.239557	83	(80.095045, -167.156232)	0.0	0	-8.9	41.1	0_0_5	80.095045	-167.156232	102.334602	-144.916675	257.478369	-167.201840
1	15	22.239557	22.239557	667	(146.813715, -167.156232)	0.0	0	-8.9	41.1	0_0_15	146.813715	-167.156232	169.053272	-144.916675	257.478369	-167.201840
2	19	22.239557	22.239557	83	(102.334602, -122.677118)	0.0	0	-8.9	41.1	0_0_19	102.334602	-122.677118	124.574159	-100.437561	257.478369	-167.201840
3	24	22.239557	22.239557	2193	(124.574159, -144.916675)	0.0	0	-8.9	41.1	0_0_24	124.574159	-144.916675	146.813716	-122.677118	257.478369	-167.201840
4	25	22.239557	22.239557	1362	(124.574159, -122.677118)	0.0	0	-8.9	41.1	0_0_25	124.574159	-122.677118	146.813716	-100.437561	257.478369	-167.201840
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
9463	124	11.273464	11.273464	73	(354.138342, 293.79397)	81.0	9	344.0	394.0	9_14_124	354.138342	293.793970	365.411806	305.067434	323.648072	193.096725
9464	125	11.273464	11.273464	250	(342.864877, 305.067434)	81.0	9	344.0	394.0	9_14_125	342.864877	305.067434	354.138341	316.340898	323.648072	193.096725
9465	126	11.273464	11.273464	513	(342.864877, 316.340899)	81.0	9	344.0	394.0	9_14_126	342.864877	316.340899	354.138341	327.614363	323.648072	193.096725
9466	127	11.273464	11.273464	152	(354.138342, 305.067434)	81.0	9	344.0	394.0	9_14_127	354.138342	305.067434	365.411806	316.340898	323.648072	193.096725
9467	128	11.273464	11.273464	83	(354.138342, 316.340899)	81.0	9	344.0	394.0	9_14_128	354.138342	316.340899	365.411806	327.614363	323.648072	193.096725

9468 rows × 16 columns

Plot QuadTree ensembles¶

In [12]:

model.gridding_plot

model.gridding_plot

Out[12]:

This shows the 10 Quadtree ensembles we made. Region with higher data volume were split into smaller gird. The grid length is constrained between (5, 25) unit.

If you set n_jobs > 1, this grid plotting may not work. But you can plot it in another way. See below.

Take a look at the ensemble grids:

In [14]:

model.ensemble_df

model.ensemble_df

Out[14]:

	stixel_indexes	stixel_width	stixel_height	stixel_checklist_count	stixel_calibration_point(transformed)	rotation	ensemble_index	DOY_start	DOY_end	unique_stixel_id	stixel_calibration_point_transformed_left_bound	stixel_calibration_point_transformed_lower_bound	stixel_calibration_point_transformed_right_bound	stixel_calibration_point_transformed_upper_bound	calibration_point_x_jitter	calibration_point_y_jitter
0	5	22.239557	22.239557	83	(80.095045, -167.156232)	0.0	0	-8.9	41.1	0_0_5	80.095045	-167.156232	102.334602	-144.916675	257.478369	-167.201840
1	15	22.239557	22.239557	667	(146.813715, -167.156232)	0.0	0	-8.9	41.1	0_0_15	146.813715	-167.156232	169.053272	-144.916675	257.478369	-167.201840
2	19	22.239557	22.239557	83	(102.334602, -122.677118)	0.0	0	-8.9	41.1	0_0_19	102.334602	-122.677118	124.574159	-100.437561	257.478369	-167.201840
3	24	22.239557	22.239557	2193	(124.574159, -144.916675)	0.0	0	-8.9	41.1	0_0_24	124.574159	-144.916675	146.813716	-122.677118	257.478369	-167.201840
4	25	22.239557	22.239557	1362	(124.574159, -122.677118)	0.0	0	-8.9	41.1	0_0_25	124.574159	-122.677118	146.813716	-100.437561	257.478369	-167.201840
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
9463	124	11.273464	11.273464	73	(354.138342, 293.79397)	81.0	9	344.0	394.0	9_14_124	354.138342	293.793970	365.411806	305.067434	323.648072	193.096725
9464	125	11.273464	11.273464	250	(342.864877, 305.067434)	81.0	9	344.0	394.0	9_14_125	342.864877	305.067434	354.138341	316.340898	323.648072	193.096725
9465	126	11.273464	11.273464	513	(342.864877, 316.340899)	81.0	9	344.0	394.0	9_14_126	342.864877	316.340899	354.138341	327.614363	323.648072	193.096725
9466	127	11.273464	11.273464	152	(354.138342, 305.067434)	81.0	9	344.0	394.0	9_14_127	354.138342	305.067434	365.411806	316.340898	323.648072	193.096725
9467	128	11.273464	11.273464	83	(354.138342, 316.340899)	81.0	9	344.0	394.0	9_14_128	354.138342	316.340899	365.411806	327.614363	323.648072	193.096725

9468 rows × 16 columns

Feature importances¶

After training the model, now we are interested in what features are important in bird abundance prediction

In [15]:

# Calcualte feature importance.
model.calculate_feature_importances()
# stixel-specific feature importance is saved in model.feature_importances_

# Calcualte feature importance. model.calculate_feature_importances() # stixel-specific feature importance is saved in model.feature_importances_

The feature importances for each stixel are calculated:

In [16]:

model.feature_importances_.sample(5)

model.feature_importances_.sample(5)

Out[16]:

	stixel_index	DOY	duration_minutes	Traveling	Stationary	Area	effort_distance_km	number_observers	obsvr_species_count	time_observation_started_minute_of_day	elevation_mean	slope_mean	eastness_mean	northness_mean	bio1	bio2	bio3	bio4	bio5	bio6	bio7	bio8	bio9	bio10	bio11	bio12	bio13	bio14	bio15	bio16	bio17	bio18	bio19	closed_shrublands	cropland_or_natural_vegetation_mosaics	croplands	deciduous_broadleaf_forests	deciduous_needleleaf_forests	evergreen_broadleaf_forests	evergreen_needleleaf_forests	grasslands	mixed_forests	non_vegetated_lands	open_shrublands	permanent_wetlands	savannas	urban_and_built_up_lands	water_bodies	woody_savannas	entropy
7302	7_13_117	0.008465	0.009498	0.014223	0.000000	0.000000	0.141843	0.015724	0.020590	1.025573e-02	0.036448	1.821750e-02	0.008884	0.014351	1.742155e-02	0.007368	0.021472	0.086128	0.012846	0.015610	0.035559	0.011594	0.015222	0.017051	0.017510	0.009545	1.816298e-02	0.022154	0.019168	0.004392	0.014175	0.007214	1.162451e-01	0.000000	0.010758	0.014279	0.037544	0.000000	0.000000	0.000000	0.002346	0.018605	0.036980	0.000000	0.039077	0.008300	0.027350	0.009089	0.017937	0.010401
5720	6_3_102	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	2.040816e-02	0.020408	2.040816e-02	0.020408	0.020408	2.040816e-02	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	2.040816e-02	0.020408	0.020408	0.020408	0.020408	0.020408	2.040816e-02	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408
5503	5_14_184	0.133284	0.014084	0.000000	0.000000	0.000000	0.053762	0.000100	0.009951	7.223156e-03	0.185217	2.487433e-02	0.009555	0.025175	1.251455e-09	0.005918	0.004731	0.004413	0.147197	0.000000	0.001148	0.020124	0.038029	0.000000	0.022076	0.006934	1.787043e-08	0.000004	0.000000	0.005954	0.001237	0.000000	1.959033e-10	0.000000	0.000000	0.000000	0.211133	0.000000	0.038666	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000006	0.015942	0.008809	0.000000	0.004452
1763	1_11_196	0.019644	0.522167	0.000000	0.000000	0.000000	0.039570	0.023542	0.026627	4.075864e-08	0.000000	1.409089e-07	0.026117	0.075152	2.854827e-02	0.004155	0.023994	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000e+00	0.000000	0.000000	0.000000	0.033747	0.000000	1.724766e-01	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.004259
7944	8_7_130	0.012785	0.030755	0.046660	0.000000	0.000000	0.026404	0.013516	0.029502	1.629446e-02	0.035024	3.039129e-02	0.112318	0.040081	9.970205e-03	0.012419	0.032699	0.037800	0.030315	0.020181	0.003512	0.012069	0.025616	0.023382	0.009851	0.022060	1.047577e-02	0.031586	0.010241	0.013239	0.021978	0.063895	1.588509e-02	0.000000	0.019851	0.013990	0.042858	0.000000	0.000000	0.012277	0.009405	0.016174	0.000000	0.000000	0.013930	0.003988	0.029067	0.005149	0.012490	0.019914

The stixel index naming follows {temporal_bin_index}_{ensemble_fold_index}_{grid_index}. For example, 17_7_103 means the 17th temporal bin, 7th ensemble, and 103th gird. The digits shown are feature importance calculated by the .feature_importances_ function of base model. Make sure your base model have one.

We can try to calculate the overall feature importance by average the ranking (or average the value directly). Notice: the assumption of this averaging is that the feature importance are homogeneous among different scales (that Quadtree generated), which may not be true.

In [17]:

top10_features = model.feature_importances_.iloc[:,1:].rank(axis=1).mean(axis=0).sort_values(ascending=False).head(10)
top10_features

top10_features = model.feature_importances_.iloc[:,1:].rank(axis=1).mean(axis=0).sort_values(ascending=False).head(10) top10_features

Out[17]:

slope_mean             33.415126
effort_distance_km     33.222510
elevation_mean         32.087726
duration_minutes       31.436992
eastness_mean          31.039823
northness_mean         30.836115
obsvr_species_count    30.242844
DOY                    30.042252
bio4                   29.702968
bio2                   28.907521
dtype: float64

Looks like slope_mean, effort_distance_km, and elevation_mean are the top 3 predictors of Mallard abundance across the sampled space and time. They indicate that sampling parameters and topography may play important role here.

Noteworthy, it is not saying that other features, like temperate, are not important. We split the data into spatiotemporal blocks, and these feature importances can only represent what is important for predicting the abundance within the stixel (at the local level), not across them.

Now we want to visualize the feature importance by mapping them to spatiotemporal points. Our query points are constructed with 1-degree length and 7-days interval:

In [18]:

# make query points
Spatio_var1 = np.arange(-180, 180, 1)
Spatio_var2 = np.arange(-90, 90, 1)
Temporal_var1 = np.arange(1, 366, 7)
new_Spatio_var1, new_Spatio_var2, new_Temporal_var1 = np.meshgrid(Spatio_var1, Spatio_var2, Temporal_var1)

Sample_ST_df = pd.DataFrame(
    {
        model.Temporal1: new_Temporal_var1.flatten(),
        model.Spatio1: new_Spatio_var1.flatten(),
        model.Spatio2: new_Spatio_var2.flatten(),
    }
)

# make query points Spatio_var1 = np.arange(-180, 180, 1) Spatio_var2 = np.arange(-90, 90, 1) Temporal_var1 = np.arange(1, 366, 7) new_Spatio_var1, new_Spatio_var2, new_Temporal_var1 = np.meshgrid(Spatio_var1, Spatio_var2, Temporal_var1) Sample_ST_df = pd.DataFrame( { model.Temporal1: new_Temporal_var1.flatten(), model.Spatio1: new_Spatio_var1.flatten(), model.Spatio2: new_Spatio_var2.flatten(), } )

In [19]:

# Assign the feature importance to spatio-temporal points of interest
importances_by_points = model.assign_feature_importances_by_points(Sample_ST_df, verbosity=1, n_jobs=1)

# Assign the feature importance to spatio-temporal points of interest importances_by_points = model.assign_feature_importances_by_points(Sample_ST_df, verbosity=1, n_jobs=1)

Querying ensembles:   0%|          | 0/10 [00:00<?, ?it/s]

Querying ensembles: 100%|██████████| 10/10 [03:01<00:00, 18.12s/it]

In [20]:

importances_by_points.head()

importances_by_points.head()

Out[20]:

	DOY	longitude	latitude	DOY_predictor	duration_minutes	Traveling	Stationary	Area	effort_distance_km	number_observers	obsvr_species_count	time_observation_started_minute_of_day	elevation_mean	slope_mean	eastness_mean	northness_mean	bio1	bio2	bio3	bio4	bio5	bio6	bio7	bio8	bio9	bio10	bio11	bio12	bio13	bio14	bio15	bio16	bio17	bio18	bio19	closed_shrublands	cropland_or_natural_vegetation_mosaics	croplands	deciduous_broadleaf_forests	deciduous_needleleaf_forests	evergreen_broadleaf_forests	evergreen_needleleaf_forests	grasslands	mixed_forests	non_vegetated_lands	open_shrublands	permanent_wetlands	savannas	urban_and_built_up_lands	water_bodies	woody_savannas	entropy
482780	22	-71	-65	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408
482886	22	-69	-65	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408
482939	22	-68	-65	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408
482992	22	-67	-65	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408
501807	22	-72	-64	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408	0.020408

In [21]:

# top 10 important variables
top_10_important_vars = importances_by_points[[
    i for i in importances_by_points.columns if not i in ['DOY','longitude','latitude']
    ]].mean().sort_values(ascending=False).head(10)

print(top_10_important_vars)

# top 10 important variables top_10_important_vars = importances_by_points[[ i for i in importances_by_points.columns if not i in ['DOY','longitude','latitude'] ]].mean().sort_values(ascending=False).head(10) print(top_10_important_vars)

DOY_predictor                             0.044851
duration_minutes                          0.038485
effort_distance_km                        0.033102
elevation_mean                            0.030670
eastness_mean                             0.029683
northness_mean                            0.028671
bio4                                      0.028083
slope_mean                                0.027811
obsvr_species_count                       0.026902
time_observation_started_minute_of_day    0.024800
dtype: float64

We see that feature importances assigned to spatiotemporal points have similar but different top-ranking features. This is expected, for different methods are used.

Ploting the feature importances by vairable names¶

We continue to visualize these feature important of dynamics:

In [22]:

from stemflow.utils.plot_gif import make_sample_gif

# make spatio-temporal GIF for top 3 variables
for var_ in top_10_important_vars.index[:3]:
    make_sample_gif(importances_by_points, f'./FTR_IPT_{var_}.gif',
                                col=var_, log_scale = False,
                                Spatio1='longitude', Spatio2='latitude', Temporal1='DOY',
                                figsize=(18,9), xlims=(-180, 180), ylims=(-90,90), grid=True,
                                xtick_interval=20, ytick_interval=20,
                                lng_size = 360, lat_size = 180, dpi=100, fps=10)

from stemflow.utils.plot_gif import make_sample_gif # make spatio-temporal GIF for top 3 variables for var_ in top_10_important_vars.index[:3]: make_sample_gif(importances_by_points, f'./FTR_IPT_{var_}.gif', col=var_, log_scale = False, Spatio1='longitude', Spatio2='latitude', Temporal1='DOY', figsize=(18,9), xlims=(-180, 180), ylims=(-90,90), grid=True, xtick_interval=20, ytick_interval=20, lng_size = 360, lat_size = 180, dpi=100, fps=10)

0.0.0.0.0.1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.
Finish!
0.0.0.0.0.1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.
Finish!
0.0.0.0.0.1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.
Finish!

In [23]:

top_10_important_vars.index[:3]

top_10_important_vars.index[:3]

Out[23]:

Index(['DOY_predictor', 'duration_minutes', 'effort_distance_km'], dtype='object')

The feature importance for vairable DOY_predictor:

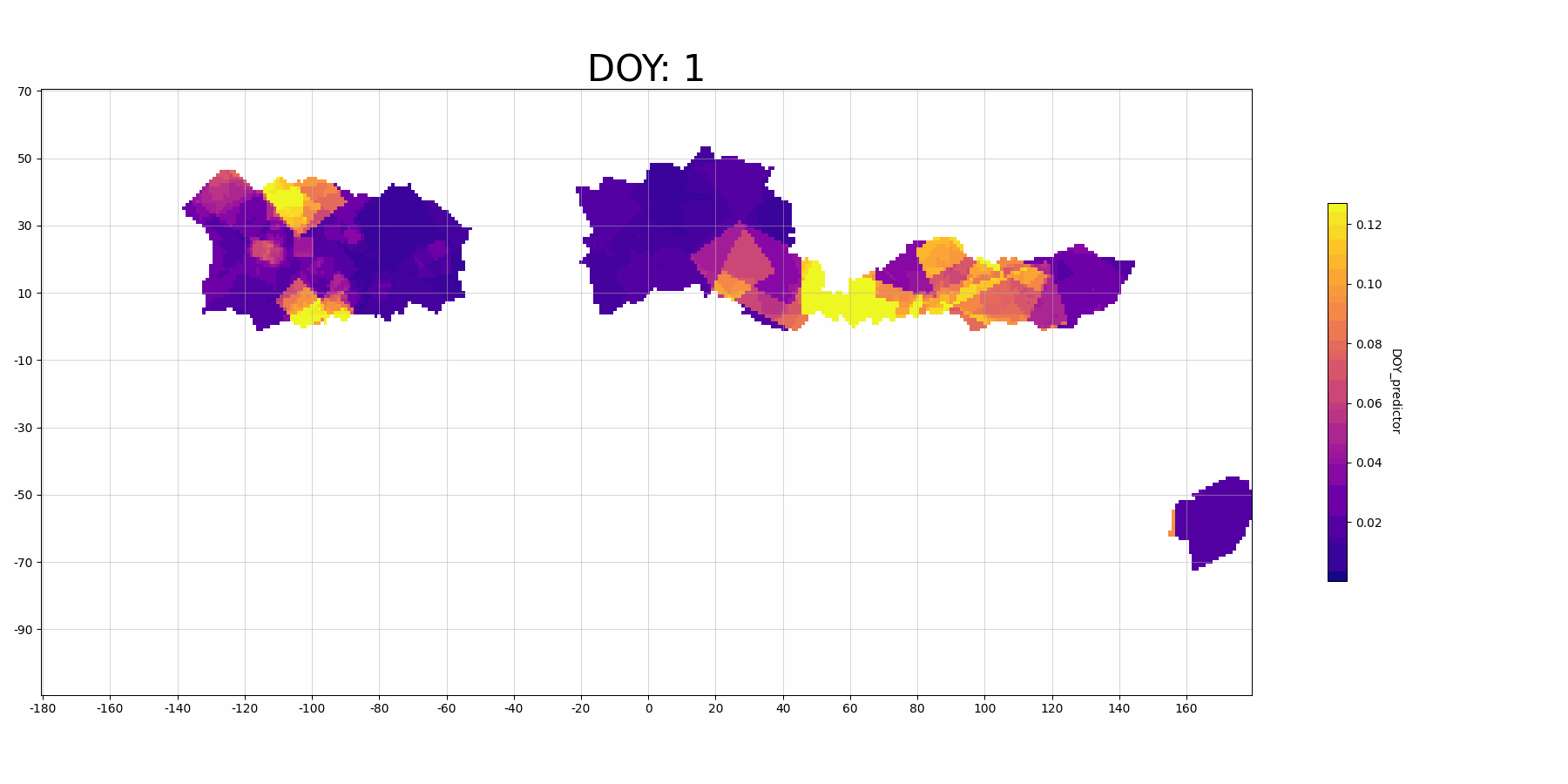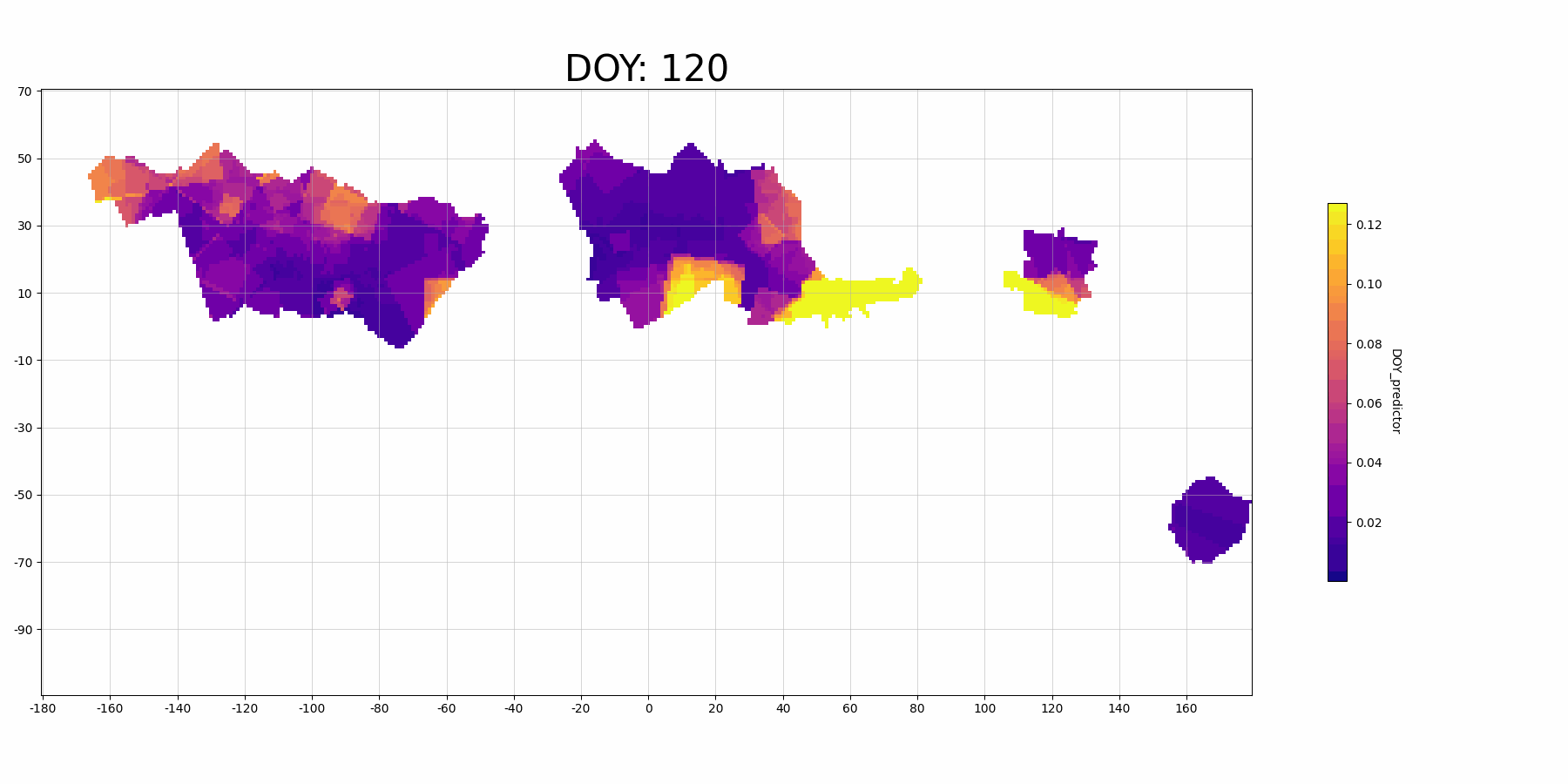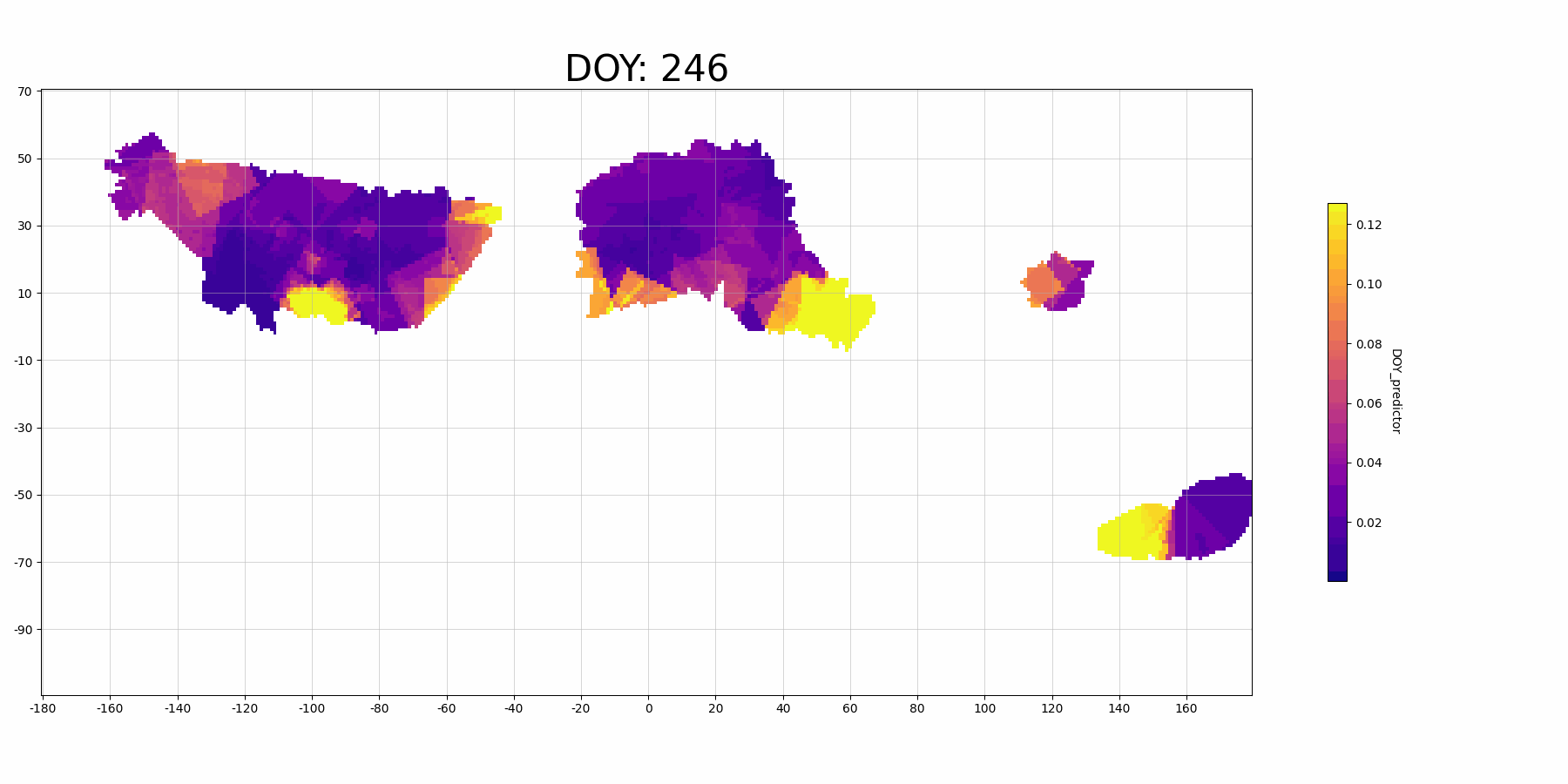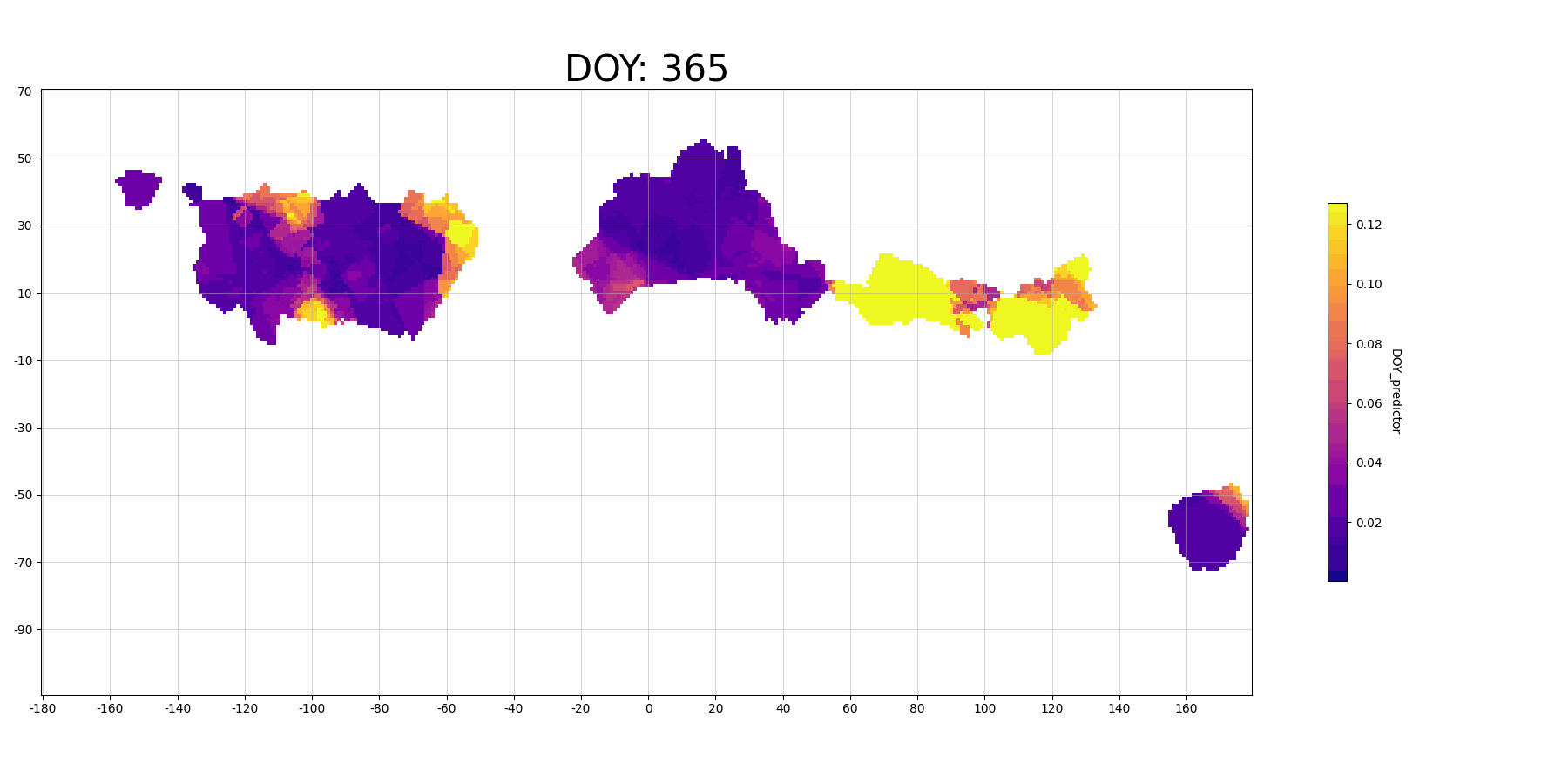
Focussing on North America (the large block on the left, longitude -160 to -40): The predictor DOY (day of year) seems to be a more important predictor during spring (30-150 DOY) than other time periods, which makes sense because spring migration is highly scheduled. And there is also higher importance in the middle migration flyway. This may indicate that there are more migrant Mallard population (since they follow the time heavily) in this regions.

Plot uncertainty in training¶

stemflow support calculating the variation of prediction across ensembles. It represent the uncertainty of making this prediction based on the surrounding information.

In [24]:

# calculate mean and standard deviation in abundance prediction
pred_mean, pred_std = model.predict(X_train.reset_index(drop=True), 
                                               return_std=True, verbosity=0, n_jobs=1)

# calculate mean and standard deviation in abundance prediction pred_mean, pred_std = model.predict(X_train.reset_index(drop=True), return_std=True, verbosity=0, n_jobs=1)

Next, we can plot these uncertainties. We visualize them by first aggregate them to hexagons using h3pandas package (you may install it if you haven't):

In [25]:

# make error_df
error_df = X_train[['longitude', 'latitude']]
error_df.columns = ['lng', 'lat']
error_df['pred_std'] = pred_std
error_df['log_pred_std'] = np.log(pred_std+1)

# Aggregate error to hexagon
import h3pandas # You can also use other aggregation method if you don't want to install h3pandas
H_level = 3
error_df = error_df.h3.geo_to_h3(H_level)
error_df = error_df.reset_index(drop=False).groupby(f'h3_0{H_level}').mean()
error_df = error_df.h3.h3_to_geo_boundary()

# make error_df error_df = X_train[['longitude', 'latitude']] error_df.columns = ['lng', 'lat'] error_df['pred_std'] = pred_std error_df['log_pred_std'] = np.log(pred_std+1) # Aggregate error to hexagon import h3pandas # You can also use other aggregation method if you don't want to install h3pandas H_level = 3 error_df = error_df.h3.geo_to_h3(H_level) error_df = error_df.reset_index(drop=False).groupby(f'h3_0{H_level}').mean() error_df = error_df.h3.h3_to_geo_boundary()

In [26]:

# plot mean uncertainty in hexagon
EU_error_df = error_df.query(
    '-30<=lng<=50 & 20<=lat<=80'
    )

EU_error_df.plot('log_pred_std', legend=True, legend_kwds={'shrink':0.7}, vmax = EU_error_df['log_pred_std'].quantile(0.9))

plt.grid(alpha=0.3)
plt.title('Log standard deviation in estimated mean abundance')
plt.xlabel('longitude')
plt.ylabel('latitude')
plt.show()

# plot mean uncertainty in hexagon EU_error_df = error_df.query( '-30<=lng<=50 & 20<=lat<=80' ) EU_error_df.plot('log_pred_std', legend=True, legend_kwds={'shrink':0.7}, vmax = EU_error_df['log_pred_std'].quantile(0.9)) plt.grid(alpha=0.3) plt.title('Log standard deviation in estimated mean abundance') plt.xlabel('longitude') plt.ylabel('latitude') plt.show()

We see a higher relative prediction uncertainty in western Europe than eastern Europe.

Likewise, you can also aggregate the pred_std based on temporal features:

In [27]:

# make error_df
error_df = X_train[['longitude', 'latitude','DOY']]
error_df['log_pred_std'] = np.log(pred_std+1)
error_df.groupby('DOY')['log_pred_std'].mean().plot()
plt.ylabel('log_pred_std')
plt.show()

# make error_df error_df = X_train[['longitude', 'latitude','DOY']] error_df['log_pred_std'] = np.log(pred_std+1) error_df.groupby('DOY')['log_pred_std'].mean().plot() plt.ylabel('log_pred_std') plt.show()

Interestingly, the prediction errors are the highest during spring and fall, when Mallards migrate, and lower during the summer and winter. It means the challenge of catching the abundance heterogeneity is larger during migration seasons.

Save model¶

If you are not using lazyloading (check model.lazy_loading), you can use pickle to save the model:

In [28]:

with open('./01.demo_adastem_model.pkl','wb') as f:
    pickle.dump(model, f)

with open('./01.demo_adastem_model.pkl','wb') as f: pickle.dump(model, f)

To load the model, do:

In [29]:

with open('./01.demo_adastem_model.pkl','rb') as f:
    model = pickle.load(f)

with open('./01.demo_adastem_model.pkl','rb') as f: model = pickle.load(f)

If you are using lazy-loading, do not save the model simply using pickle, because it will not save the ensembles stored on the disk.

Otherwise if you are using lazy_loading=True, try:

In [30]:

model.save(tar_gz_file='./my_model.tar.gz', remove_temporary_file=True) 
# After removing temporary files, you can no longer access to the ensembles saved on disk!
# Instead, they are in the .tar.gz file no2.

model.save(tar_gz_file='./my_model.tar.gz', remove_temporary_file=True) # After removing temporary files, you can no longer access to the ensembles saved on disk! # Instead, they are in the .tar.gz file no2.

In [33]:

# Load model
model = AdaSTEM.load(tar_gz_file='./my_model.tar.gz', new_lazy_loading_path='./new_lazyloading_ensemble_folder', remove_original_file=False)
# If not specifying target_lazyloading_path, a random folder will be made under your current working directory.

# Load model model = AdaSTEM.load(tar_gz_file='./my_model.tar.gz', new_lazy_loading_path='./new_lazyloading_ensemble_folder', remove_original_file=False) # If not specifying target_lazyloading_path, a random folder will be made under your current working directory.

In [34]:

model.lazy_loading_dir # notice that your lazy loading folder now is changed!

model.lazy_loading_dir # notice that your lazy loading folder now is changed!

Out[34]:

'new_lazyloading_ensemble_folder'

Make sure you use the same version of stemflow for write and load models

Evaluation¶

Now, we evaluate our overall model performance on the held-out test set:

In [35]:

pred = model.predict(X_test, verbosity=1)

pred = model.predict(X_test, verbosity=1)

Predicting: 100%|██████████| 10/10 [00:26<00:00,  2.70s/it]

The samples not predictable are output as np.nan:

In [36]:

perc = np.sum(np.isnan(pred.flatten()))/len(pred.flatten())
print(f'Percentage not predictable {round(perc*100, 2)}%')

perc = np.sum(np.isnan(pred.flatten()))/len(pred.flatten()) print(f'Percentage not predictable {round(perc*100, 2)}%')

Percentage not predictable 1.08%

AdaSTEM is relatively conservative compare to other models like Maxent, gradient boosting, or linear regression – It ameliorates the long-distance/long-range prediction problem. Consequently, there are 0.56% percent of test samples that cannot be predicted by our model, based on the configuration that they have to have 7 ensembles covered (set when we created the model). These samples are too far way from the "knowledge zone" that we trained on in terms of space and time.

We evaluate the performance using various metrics implemented in AdaSTEM.eval_STEM_res method:

In [37]:

pred_df = pd.DataFrame({
    'y_true':y_test.flatten(),
    'y_pred':np.where(pred.flatten()<0, 0, pred.flatten())
}).dropna()

AdaSTEM.eval_STEM_res('hurdle', pred_df.y_true, pred_df.y_pred)

pred_df = pd.DataFrame({ 'y_true':y_test.flatten(), 'y_pred':np.where(pred.flatten()<0, 0, pred.flatten()) }).dropna() AdaSTEM.eval_STEM_res('hurdle', pred_df.y_true, pred_df.y_pred)

Out[37]:

{'AUC': 0.7657828013347322,
 'kappa': 0.39316454503252696,
 'f1': 0.5235653147459279,
 'precision': 0.4012566082648288,
 'recall': 0.7531300327289729,
 'average_precision': 0.34285479100958616,
 'Spearman_r': 0.467379209762645,
 'Pearson_r': 0.14676280568818745,
 'R2': 0.0006978801246821931,
 'MAE': 4.3229564451692575,
 'MSE': 3569.7235263193556,
 'poisson_deviance_explained': 0.2003715565172579}

The AUC reach 0.77, which is acceptable considering the quality of citizen science data. The recall is higher than precision, as expected. But R2 is low and MAE/MSE are high. This indicate that our model is good at classification, but the abundance output is not that good for downstream analysis.

Compared to simple Hurdle model¶

What if we do not use AdaSTEM, instead, use a simple hurdle model with XGB base model?

In [38]:

model2 = Hurdle(classifier=XGBClassifier(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1),
                regressor=XGBRegressor(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1))
model2.fit(X_train.drop(['longitude','latitude'], axis=1), y_train)
pred2 = model2.predict(X_test.drop(['longitude','latitude'], axis=1))

AdaSTEM.eval_STEM_res('hurdle', y_test.flatten(), np.where(pred2.flatten()<0, 0, pred2.flatten()))

model2 = Hurdle(classifier=XGBClassifier(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1), regressor=XGBRegressor(tree_method='hist',random_state=42, verbosity = 0, n_jobs=1)) model2.fit(X_train.drop(['longitude','latitude'], axis=1), y_train) pred2 = model2.predict(X_test.drop(['longitude','latitude'], axis=1)) AdaSTEM.eval_STEM_res('hurdle', y_test.flatten(), np.where(pred2.flatten()<0, 0, pred2.flatten()))

Out[38]:

{'AUC': 0.6082049353263714,
 'kappa': 0.28979249306499655,
 'f1': 0.35259024316568494,
 'precision': 0.6521860595055176,
 'recall': 0.24160413971539457,
 'average_precision': 0.2816092075882183,
 'Spearman_r': 0.343858859200218,
 'Pearson_r': 0.1318304214931483,
 'R2': 0.00808413693181853,
 'MAE': 4.120743585028297,
 'MSE': 3506.544713065713,
 'poisson_deviance_explained': 0.15941000851892428}

The untuned naive hurdle model did not out perform the AdaSTEM model, in terms of both classification metrics and regression metrics, which proves the advantages of using AdaSTEM framework.

Prediction¶

Now our model can show its full power: Making prediction

We first load the prediction set downloaded from https://figshare.com/articles/dataset/Predset_2020_csv/24124980 :

In [39]:

pred_set = pd.read_csv('./Predset_2020.csv')

pred_set = pd.read_csv('./Predset_2020.csv')

For simplicity, we did not predict on the full set – Instead, we subsample the prediction set to 500 x 500 grids across the world, with one point per gird:

In [40]:

## reduce the prediction size
pred_set['lng_grid'] = np.digitize(
    pred_set.longitude,
    np.linspace(-180,180,500)
)

pred_set['lat_grid'] = np.digitize(
    pred_set.latitude,
    np.linspace(-90,90,500)
)

pred_set = pred_set.sample(frac=1, replace=False).groupby(['lng_grid','lat_grid']).first().reset_index(drop=True)
# pred_set = pred_set.drop(['lng_grid','lat_grid'], axis=1)

## reduce the prediction size pred_set['lng_grid'] = np.digitize( pred_set.longitude, np.linspace(-180,180,500) ) pred_set['lat_grid'] = np.digitize( pred_set.latitude, np.linspace(-90,90,500) ) pred_set = pred_set.sample(frac=1, replace=False).groupby(['lng_grid','lat_grid']).first().reset_index(drop=True) # pred_set = pred_set.drop(['lng_grid','lat_grid'], axis=1)

Then we can make our prediction. As mention before, the only dynamic feature in our model is DOY. To predict the abundance for each day, we only need to set the DOY to the target day. Additionally, we define the relative abundance prediction as

"A birder (number_observers=1)
who has observed 500 species (obsvr_species_count=500) in the past,
traveling 1km (Traveling=1; effort_distance_km=1)
within one hour (duration_minutes=60)
at 7:00 in the morning (time_observation_started_minute_of_day=420),
how many Mallard will they observe"

In [ ]:

pred_df = []
for doy in tqdm(range(1,367)):
    pred_set['DOY'] = doy
    pred_set['duration_minutes'] = 60
    pred_set['Traveling'] = 1
    pred_set['Stationary'] = 0
    pred_set['Area'] = 0
    pred_set['effort_distance_km'] = 1
    pred_set['number_observers'] = 1
    pred_set['obsvr_species_count'] = 500
    pred_set['time_observation_started_minute_of_day'] = 420
    pred = model.predict(pred_set.fillna(-1), verbosity=0)
    
    pred_df.append(pd.DataFrame({
        'longitude':pred_set.longitude.values,
        'latitude':pred_set.latitude.values,
        'DOY':doy,
        'pred':np.array(pred).flatten()
    }))
    
    not_p = np.sum(np.isnan(pred.flatten()))/len(pred.flatten())
    # print(f'DOY {doy} Not predictable: {not_p*100}%')

pred_df = [] for doy in tqdm(range(1,367)): pred_set['DOY'] = doy pred_set['duration_minutes'] = 60 pred_set['Traveling'] = 1 pred_set['Stationary'] = 0 pred_set['Area'] = 0 pred_set['effort_distance_km'] = 1 pred_set['number_observers'] = 1 pred_set['obsvr_species_count'] = 500 pred_set['time_observation_started_minute_of_day'] = 420 pred = model.predict(pred_set.fillna(-1), verbosity=0) pred_df.append(pd.DataFrame({ 'longitude':pred_set.longitude.values, 'latitude':pred_set.latitude.values, 'DOY':doy, 'pred':np.array(pred).flatten() })) not_p = np.sum(np.isnan(pred.flatten()))/len(pred.flatten()) # print(f'DOY {doy} Not predictable: {not_p*100}%')

  0%|          | 0/366 [00:00<?, ?it/s]

In [ ]:

pred_df = pd.concat(pred_df, axis=0)
pred_df['pred'] = np.where(pred_df['pred']<0, 0, pred_df['pred'])

pred_df = pd.concat(pred_df, axis=0) pred_df['pred'] = np.where(pred_df['pred']<0, 0, pred_df['pred'])

We set the prediction <0 to 0, because bird count cannot be negative.

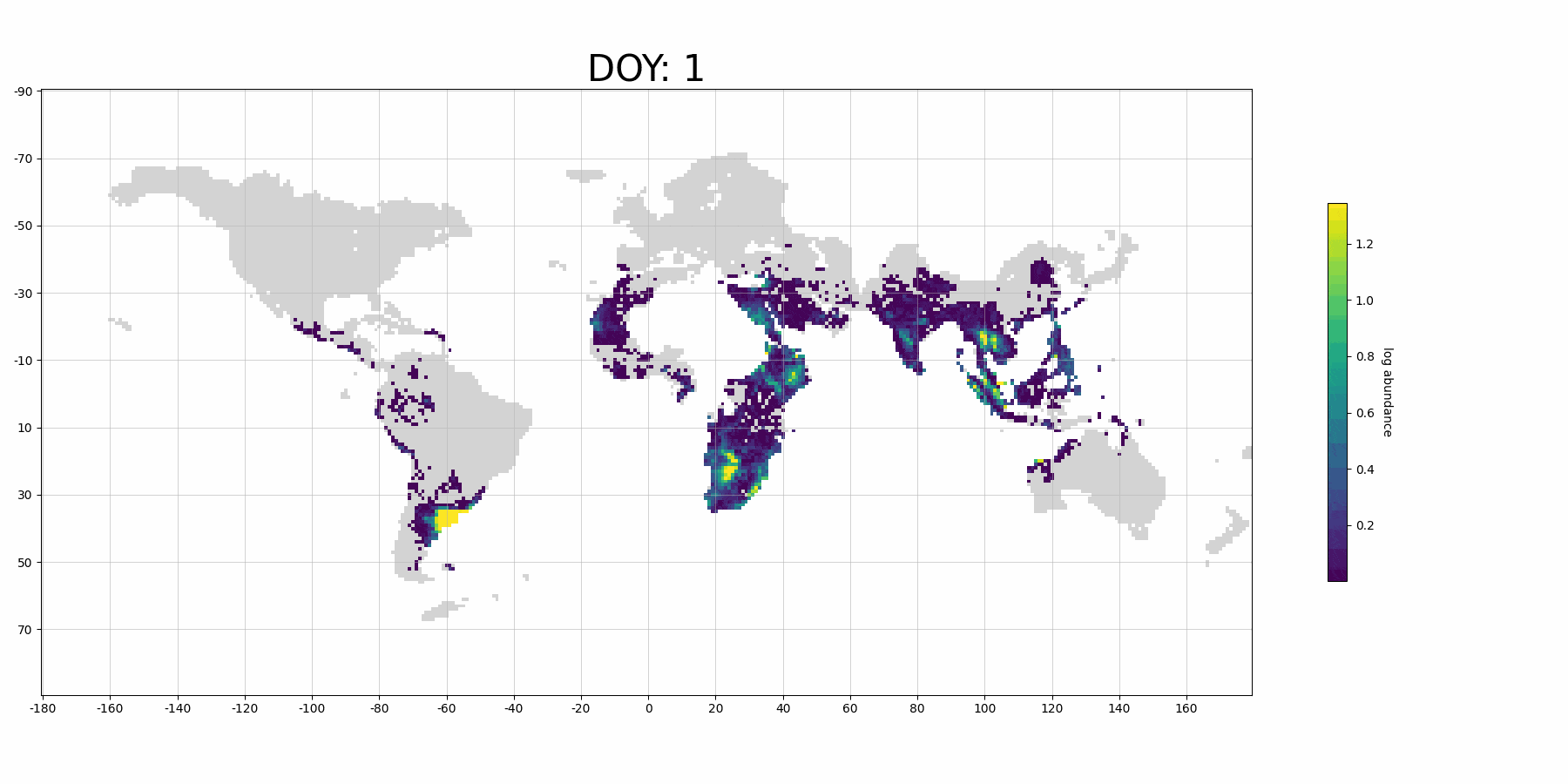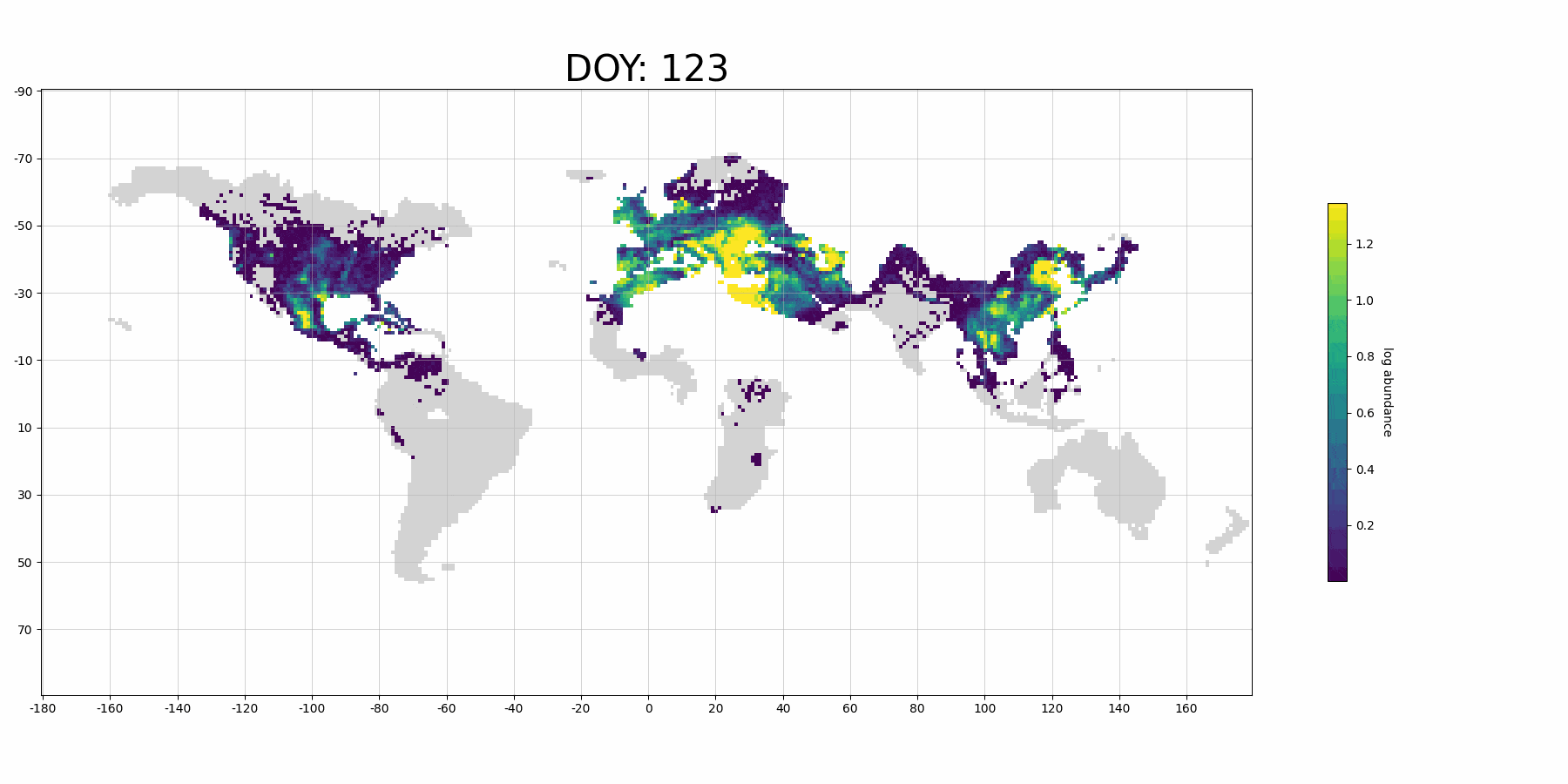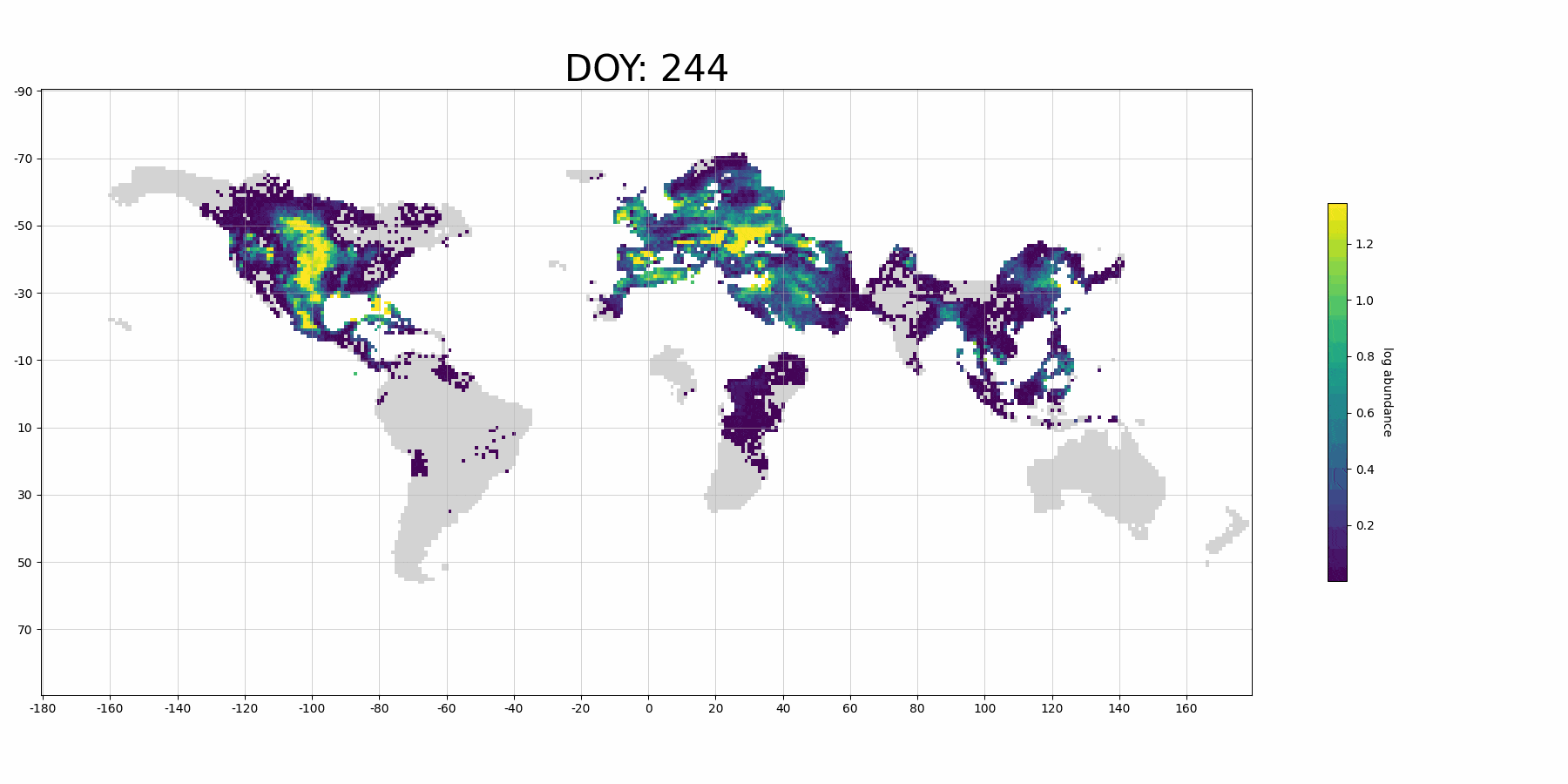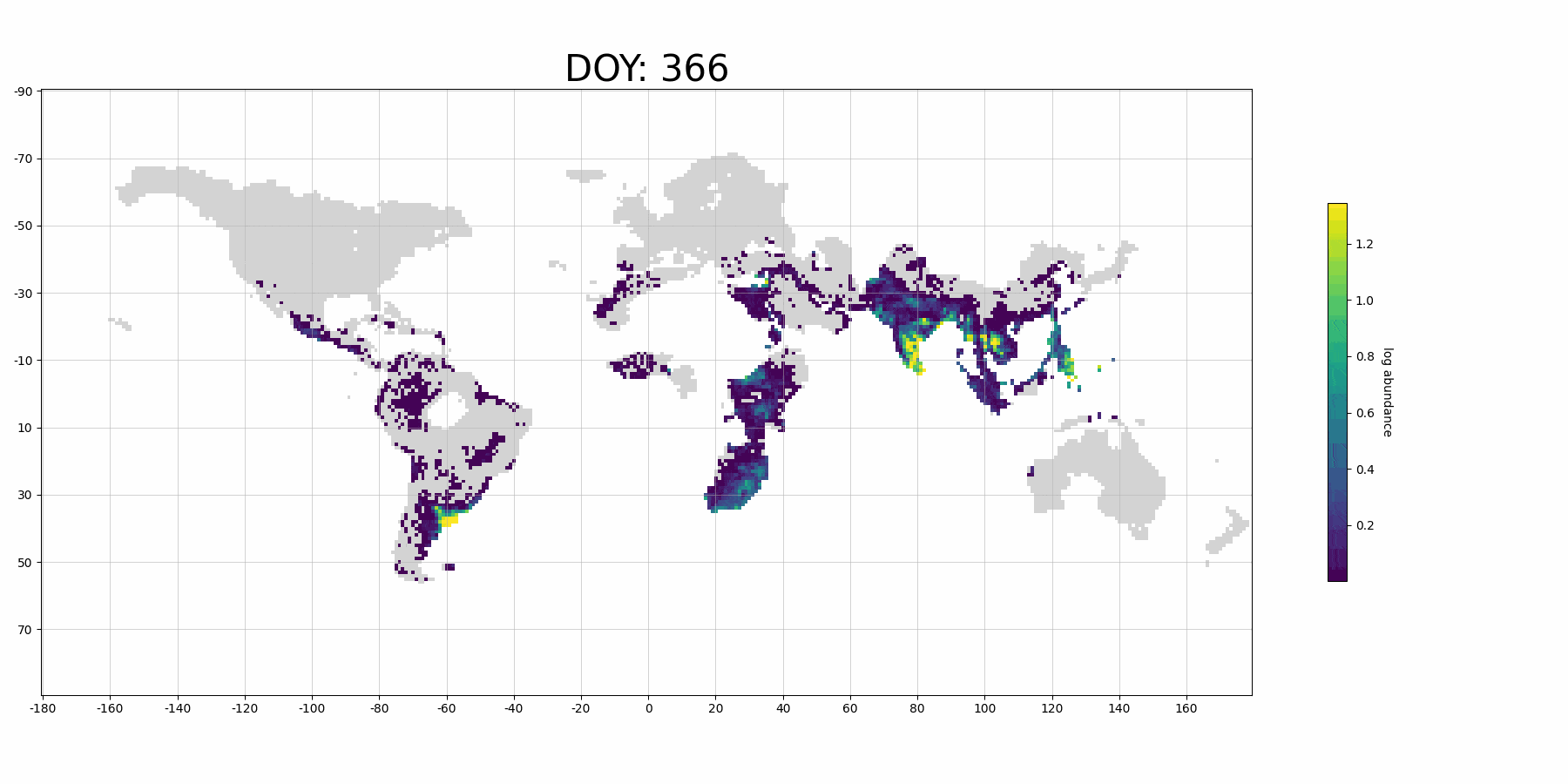
Next, we plot our prediction on map:

In [ ]:

from stemflow.utils.plot_gif import make_sample_gif
make_sample_gif(pred_df, './pred_gif_demo.gif',
                            col='pred', log_scale = True,
                            Spatio1='longitude', Spatio2='latitude', Temporal1='DOY',
                            vmin=0.0001, vmax=pred_df['pred'].dropna().quantile(0.9),
                            cmap='viridis',
                            figsize=(18,9), xlims=(-180, 180), ylims=(-90,90), grid=True,
                            xtick_interval=20, ytick_interval=20,
                            lng_size = 360, lat_size = 180, dpi=100, fps=30)

from stemflow.utils.plot_gif import make_sample_gif make_sample_gif(pred_df, './pred_gif_demo.gif', col='pred', log_scale = True, Spatio1='longitude', Spatio2='latitude', Temporal1='DOY', vmin=0.0001, vmax=pred_df['pred'].dropna().quantile(0.9), cmap='viridis', figsize=(18,9), xlims=(-180, 180), ylims=(-90,90), grid=True, xtick_interval=20, ytick_interval=20, lng_size = 360, lat_size = 180, dpi=100, fps=30)

0.0.0.0.0.1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107.108.109.110.111.112.113.114.115.116.117.118.119.120.121.122.123.124.125.126.127.128.129.130.131.132.133.134.135.136.137.138.139.140.141.142.143.144.145.146.147.148.149.150.151.152.153.154.155.156.157.158.159.160.161.162.163.164.165.166.167.168.169.170.171.172.173.174.175.176.177.178.179.180.181.182.183.184.185.186.187.188.189.190.191.192.193.194.195.196.197.198.199.200.201.202.203.204.205.206.207.208.209.210.211.212.213.214.215.216.217.218.219.220.221.222.223.224.225.226.227.228.229.230.231.232.233.234.235.236.237.238.239.240.241.242.243.244.245.246.247.248.249.250.251.252.253.254.255.256.257.258.259.260.261.262.263.264.265.266.267.268.269.270.271.272.273.274.275.276.277.278.279.280.281.282.283.284.285.286.287.288.289.290.291.292.293.294.295.296.297.298.299.300.301.302.303.304.305.306.307.308.309.310.311.312.313.314.315.316.317.318.319.320.321.322.323.324.325.326.327.328.329.330.331.332.333.334.335.336.337.338.339.340.341.342.343.344.345.346.347.348.349.350.351.352.353.354.355.356.357.358.359.360.361.362.363.364.365.
Finish!

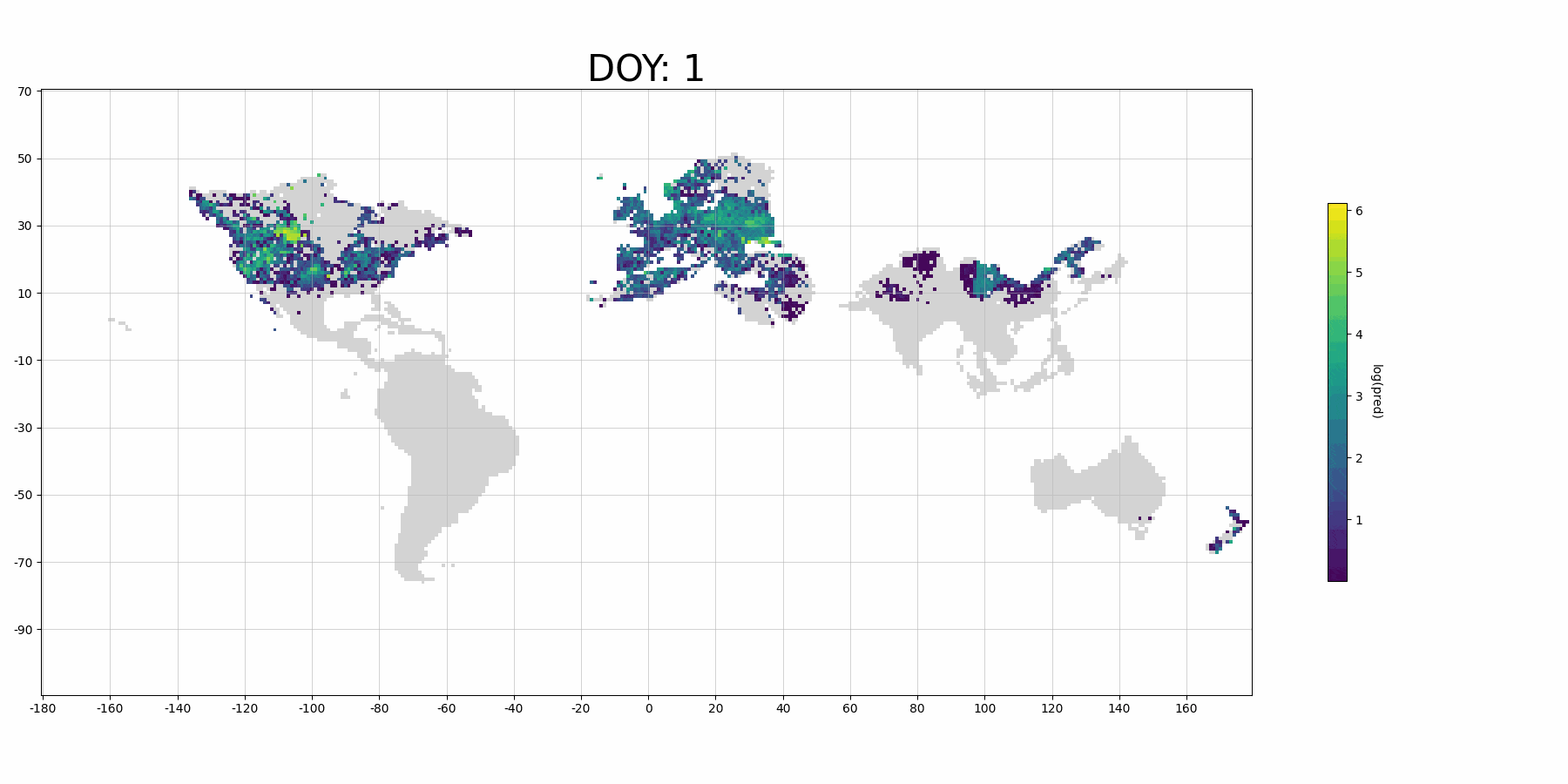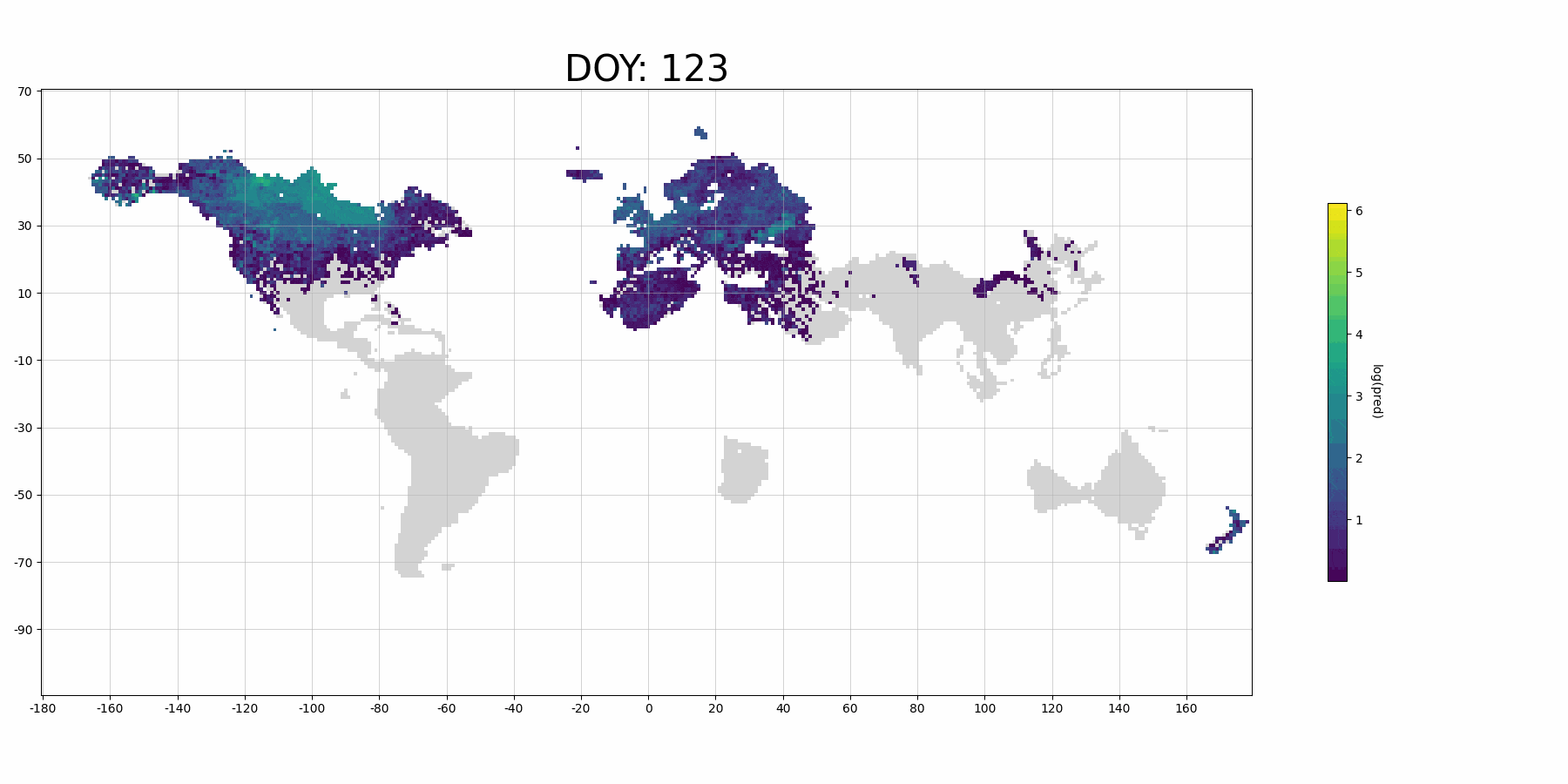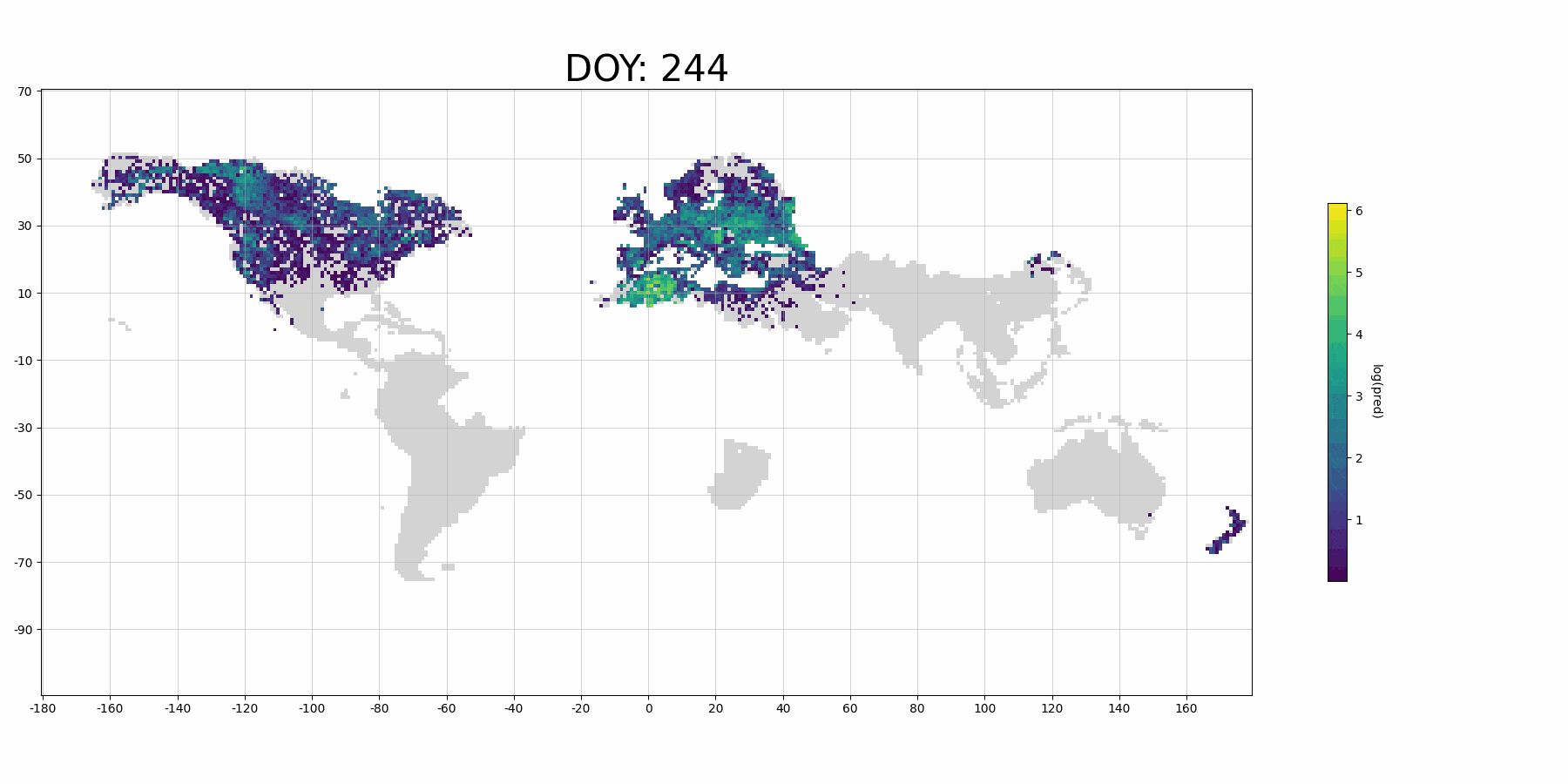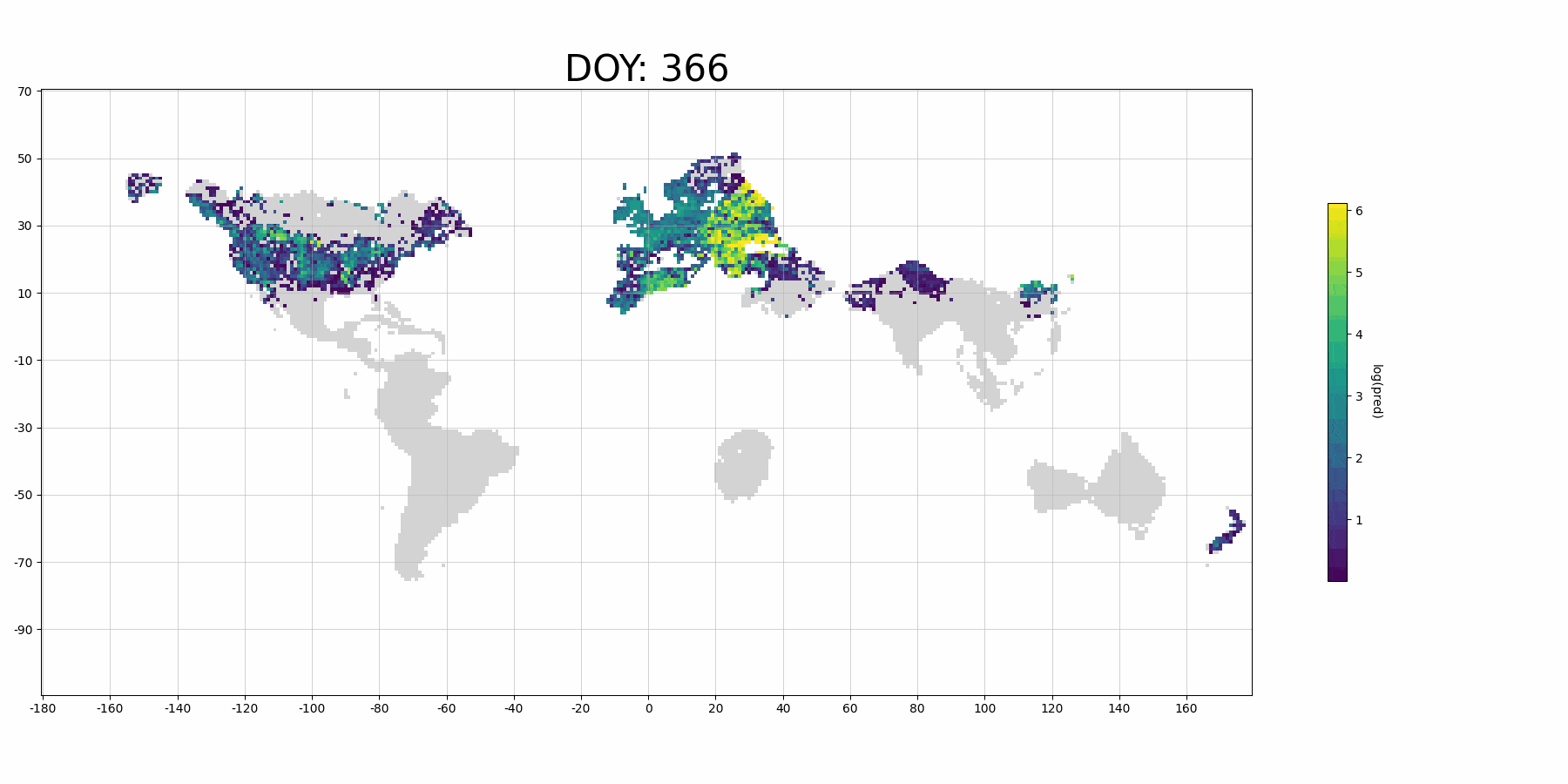
If you use more data for training and denser prediction set for visualization, it will probably look like (although it's for Barn Swallow):

Calculate memory usage¶

Finally, we are interested in how many disk space & memory our model consumed. stemflow is typically memory costly, especially when data volume and ensembles go up – the memory usage may also go up linearly. We do not currently provide solution for memory optimization. We well come PR to work on that.

In [ ]:

# Calculate memory usage
model_size_G = round(os.path.getsize('./01.demo_adastem_model.pkl')/1024/1024/1024, 2)
training_data_memory_G = round(X.memory_usage().sum()/1024/1024/1024, 2)

# Calculate model info
true_hurdle_model_count = np.sum([1 if isinstance(model.model_dict[i].classifier, XGBClassifier) else 0 for i in model.model_dict])
dummy_model_count = len(model.model_dict) - true_hurdle_model_count
true_hurdle_model_perc = round(true_hurdle_model_count/len(model.model_dict) * 100, 2)
dummy_model_perc = round(dummy_model_count/len(model.model_dict) * 100, 2)

# Calculate memory usage model_size_G = round(os.path.getsize('./01.demo_adastem_model.pkl')/1024/1024/1024, 2) training_data_memory_G = round(X.memory_usage().sum()/1024/1024/1024, 2) # Calculate model info true_hurdle_model_count = np.sum([1 if isinstance(model.model_dict[i].classifier, XGBClassifier) else 0 for i in model.model_dict]) dummy_model_count = len(model.model_dict) - true_hurdle_model_count true_hurdle_model_perc = round(true_hurdle_model_count/len(model.model_dict) * 100, 2) dummy_model_perc = round(dummy_model_count/len(model.model_dict) * 100, 2)

In [ ]:

print(f"""
      
      This AdaSTEM model have {len(model.model_dict)} trained based models in total.
      Among them, {dummy_model_count} ({dummy_model_perc}%) are dummy models that always predict one class (because the input data labels are homogeneous).
      Oppositely, {true_hurdle_model_count} ({true_hurdle_model_perc}%) are true hurdle models.
      
      The input data consume {training_data_memory_G} G memory.
      The model takes {model_size_G} G space on the disks.
      
""")

print(f""" This AdaSTEM model have {len(model.model_dict)} trained based models in total. Among them, {dummy_model_count} ({dummy_model_perc}%) are dummy models that always predict one class (because the input data labels are homogeneous). Oppositely, {true_hurdle_model_count} ({true_hurdle_model_perc}%) are true hurdle models. The input data consume {training_data_memory_G} G memory. The model takes {model_size_G} G space on the disks. """)

      
      This AdaSTEM model have 9659 trained based models in total.
      Among them, 2721 (28.17%) are dummy models that always predict one class (because the input data labels are homogeneous).
      Oppositely, 6938 (71.83%) are true hurdle models.
      
      The input data consume 0.15 G memory.
      The model takes 1.87 G space on the disks.
      

If using lazy_loading=True, the total model amount will not change, but the memory consumption will significantly decrease, and the prediction will be slower.

Other potentially useful functions¶

01. Obtaining spatial objects of stixels¶

Although for now stemflow doesn't have an internal function to obtain the spatial objects of stixels, one can realize it by:

In [ ]:

from stemflow.utils.jitterrotation.jitterrotator import JitterRotator
from shapely.geometry import Polygon
import geopandas as gpd
# Remember to install shapely and geopandas if you haven't

# define a function
def geo_grid_geometry(line):
    old_x, old_y = JitterRotator.inverse_jitter_rotate(
        [line['stixel_calibration_point_transformed_left_bound'], line['stixel_calibration_point_transformed_left_bound'], line['stixel_calibration_point_transformed_right_bound'], line['stixel_calibration_point_transformed_right_bound']],
        [line['stixel_calibration_point_transformed_lower_bound'], line['stixel_calibration_point_transformed_upper_bound'], line['stixel_calibration_point_transformed_upper_bound'], line['stixel_calibration_point_transformed_lower_bound']],
        line['rotation'],
        line['calibration_point_x_jitter'],
        line['calibration_point_y_jitter'],
    )

    polygon = Polygon(list(zip(old_x, old_y)))
    return polygon

# Make a geometry attribute for each stixel
model.ensemble_df['geometry'] = model.ensemble_df.apply(geo_grid_geometry, axis=1)
model.ensemble_df = gpd.GeoDataFrame(model.ensemble_df, geometry='geometry')

from stemflow.utils.jitterrotation.jitterrotator import JitterRotator from shapely.geometry import Polygon import geopandas as gpd # Remember to install shapely and geopandas if you haven't # define a function def geo_grid_geometry(line): old_x, old_y = JitterRotator.inverse_jitter_rotate( [line['stixel_calibration_point_transformed_left_bound'], line['stixel_calibration_point_transformed_left_bound'], line['stixel_calibration_point_transformed_right_bound'], line['stixel_calibration_point_transformed_right_bound']], [line['stixel_calibration_point_transformed_lower_bound'], line['stixel_calibration_point_transformed_upper_bound'], line['stixel_calibration_point_transformed_upper_bound'], line['stixel_calibration_point_transformed_lower_bound']], line['rotation'], line['calibration_point_x_jitter'], line['calibration_point_y_jitter'], ) polygon = Polygon(list(zip(old_x, old_y))) return polygon # Make a geometry attribute for each stixel model.ensemble_df['geometry'] = model.ensemble_df.apply(geo_grid_geometry, axis=1) model.ensemble_df = gpd.GeoDataFrame(model.ensemble_df, geometry='geometry')

Which creates a spatial object for each stixel.

In [ ]:

model.ensemble_df.plot(alpha=0.2)

model.ensemble_df.plot(alpha=0.2)

Out[ ]:

<Axes: >

The stixels will stack on the temporal dimension. You may want to pick only one time range (since the spatial splitting pattern will be the same for all temporal windows in one ensemble).

In [ ]:

model.ensemble_df[
        (model.ensemble_df['DOY_start']>=90) & (model.ensemble_df['DOY_start']<120)
].plot(alpha=0.2)

model.ensemble_df[ (model.ensemble_df['DOY_start']>=90) & (model.ensemble_df['DOY_start']<120) ].plot(alpha=0.2)

Out[ ]:

<Axes: >

Which will look less messy.

You may also want to add scatter points on top of this:

In [ ]:

fig,ax = plt.subplots()

model.ensemble_df[
        (model.ensemble_df['DOY_start']>=90) & ((model.ensemble_df['DOY_start']<120))
].plot(alpha=0.2,ax=ax)

ax.scatter(
        X_train['longitude'],
        X_train['latitude'],
        c='tab:orange',s=0.2,alpha=0.7
)

plt.show()

fig,ax = plt.subplots() model.ensemble_df[ (model.ensemble_df['DOY_start']>=90) & ((model.ensemble_df['DOY_start']<120)) ].plot(alpha=0.2,ax=ax) ax.scatter( X_train['longitude'], X_train['latitude'], c='tab:orange',s=0.2,alpha=0.7 ) plt.show()

Output to geojson: https://geopandas.org/en/stable/docs/reference/api/geopandas.GeoDataFrame.to_json.html

02. Interactive visualization of predicted results¶

In [50]:

import geoviews as gv
import geoviews.feature as gf
from cartopy import crs
import xarray as xr
gv.extension('bokeh', 'matplotlib')

# This requires installing geoviews, cartopy, and xarray if you haven't

# Make an xarray
pred_df_dropna = pred_df.dropna()
pred_df_dropna['log_pred'] = np.log(pred_df_dropna['pred'] + 1)
ds = pred_df_dropna.set_index(['latitude','longitude','DOY'])[['log_pred']].to_xarray()

# Aggregate to coarser resolution
ds = ds.coarsen(latitude=10,longitude=10,boundary='pad').mean()

# Fill the "no data" pixels for plotting (required by geroviews)
delta_latitude = float(ds['latitude'][1] - ds['latitude'][0])
delta_longitude = float(ds['longitude'][1] - ds['longitude'][0])
new_lats = np.linspace(-90, 90, int(180/delta_latitude))  # 1 degree resolution, adjust if needed
new_lons = np.linspace(-180, 180, int(360/delta_longitude))  # 1 degree resolution, adjust if needed
extended_ds = ds.reindex(latitude=new_lats, longitude=new_lons, method='nearest')

# plotting
dataset = gv.Dataset(extended_ds, 
                     ['longitude', 'latitude', 'DOY'], 
                     'log_pred', 
                     crs=crs.PlateCarree())
images = dataset.to(gv.Image)

images.opts(cmap='viridis', colorbar=True, width=900, height=450, projection=crs.Robinson()) * gf.coastline

# results are not shown due to the large size

import geoviews as gv import geoviews.feature as gf from cartopy import crs import xarray as xr gv.extension('bokeh', 'matplotlib') # This requires installing geoviews, cartopy, and xarray if you haven't # Make an xarray pred_df_dropna = pred_df.dropna() pred_df_dropna['log_pred'] = np.log(pred_df_dropna['pred'] + 1) ds = pred_df_dropna.set_index(['latitude','longitude','DOY'])[['log_pred']].to_xarray() # Aggregate to coarser resolution ds = ds.coarsen(latitude=10,longitude=10,boundary='pad').mean() # Fill the "no data" pixels for plotting (required by geroviews) delta_latitude = float(ds['latitude'][1] - ds['latitude'][0]) delta_longitude = float(ds['longitude'][1] - ds['longitude'][0]) new_lats = np.linspace(-90, 90, int(180/delta_latitude)) # 1 degree resolution, adjust if needed new_lons = np.linspace(-180, 180, int(360/delta_longitude)) # 1 degree resolution, adjust if needed extended_ds = ds.reindex(latitude=new_lats, longitude=new_lons, method='nearest') # plotting dataset = gv.Dataset(extended_ds, ['longitude', 'latitude', 'DOY'], 'log_pred', crs=crs.PlateCarree()) images = dataset.to(gv.Image) images.opts(cmap='viridis', colorbar=True, width=900, height=450, projection=crs.Robinson()) * gf.coastline # results are not shown due to the large size

The output should look like the following (interactively zoom-in and -out):

In [ ]:

import holoviews as hv
hv.save(images,'prediction_visualization.html')
# This could be a 100MB + large file. Then you can open it in a browser.

import holoviews as hv hv.save(images,'prediction_visualization.html') # This could be a 100MB + large file. Then you can open it in a browser.

Concluding mark¶

Please open an issue if you have any question

Cheers!

In [2]:

from watermark import watermark
print(watermark())
print(watermark(packages="stemflow,numpy,scipy,pandas,xgboost,tqdm,matplotlib,h3pandas,geopandas,scikit-learn"))

from watermark import watermark print(watermark()) print(watermark(packages="stemflow,numpy,scipy,pandas,xgboost,tqdm,matplotlib,h3pandas,geopandas,scikit-learn"))

Last updated: 2024-10-27T16:11:15.556933-05:00

Python implementation: CPython
Python version       : 3.11.10
IPython version      : 8.22.1

Compiler    : Clang 17.0.6 
OS          : Darwin
Release     : 23.1.0
Machine     : arm64
Processor   : arm
CPU cores   : 14
Architecture: 64bit

stemflow    : 1.1.2
numpy       : 1.26.4
scipy       : 1.14.1
pandas      : 2.2.3
xgboost     : 2.0.3
tqdm        : 4.66.5
matplotlib  : 3.9.2
h3pandas    : 0.2.6
geopandas   : 0.14.3
scikit-learn: 1.5.2